ODEs
Requires Symbolic Math Toolbox
Important Solving ODEs in Matlab is a vast and complex area of work and sometimes some ODEs won’t get solved analytically and will have to be solved numerically. If you are interested on how to do so please have a look a the Numerically solve ordinary differential equations course. The following examples will look at how to solve relatively simple ODEs analytically.
Solving the following nonlinear first order differential equation :
\[(\frac{dy}{ {dt}} + y)^2 = 1\]with an initial condition
\[y(0) = 0\]-
First declare the function y(t) as a symbolic entity
syms y(t) - Define your ODE
ode = (diff(y,t) + y)^2 == 1 - Define your condition
cond = y(0) == 0 - Compute solution using ODE and condition
ySol(t) = dsolve(ode,cond)Which results on two solutions \(y(t) = e^{-t} - 1\)
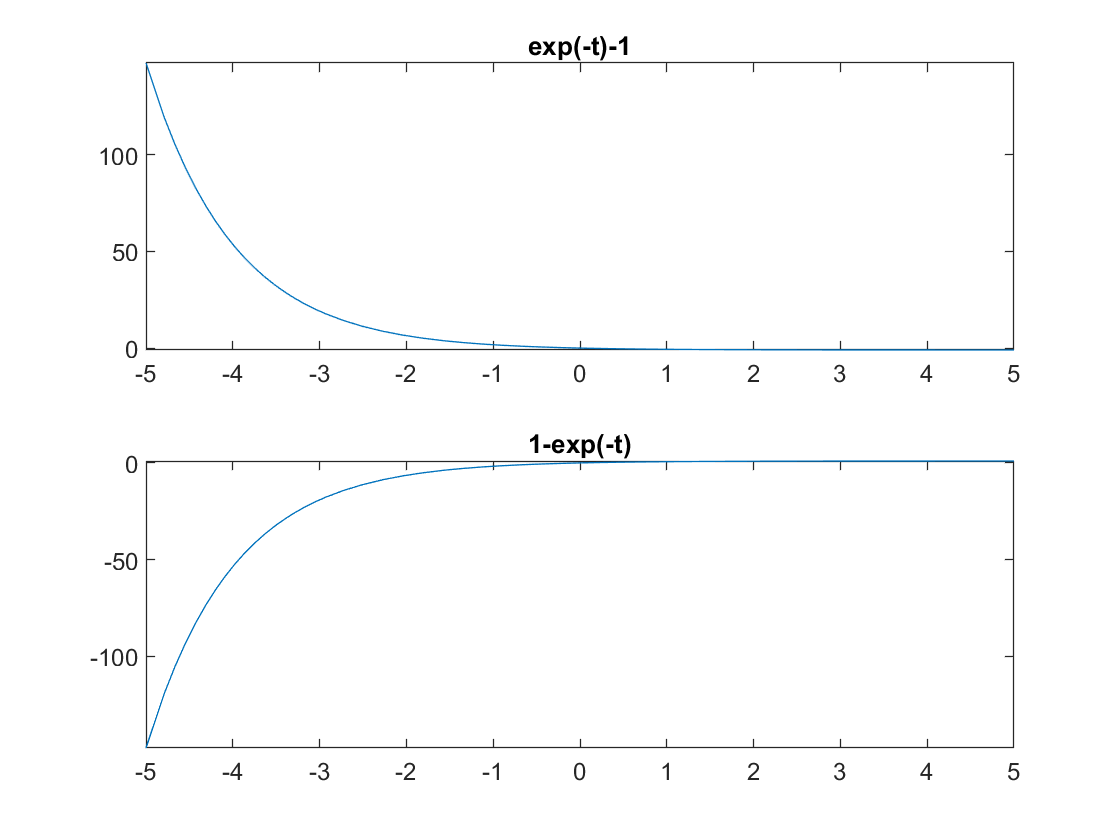
Solving second order ODEs with initial conditions:
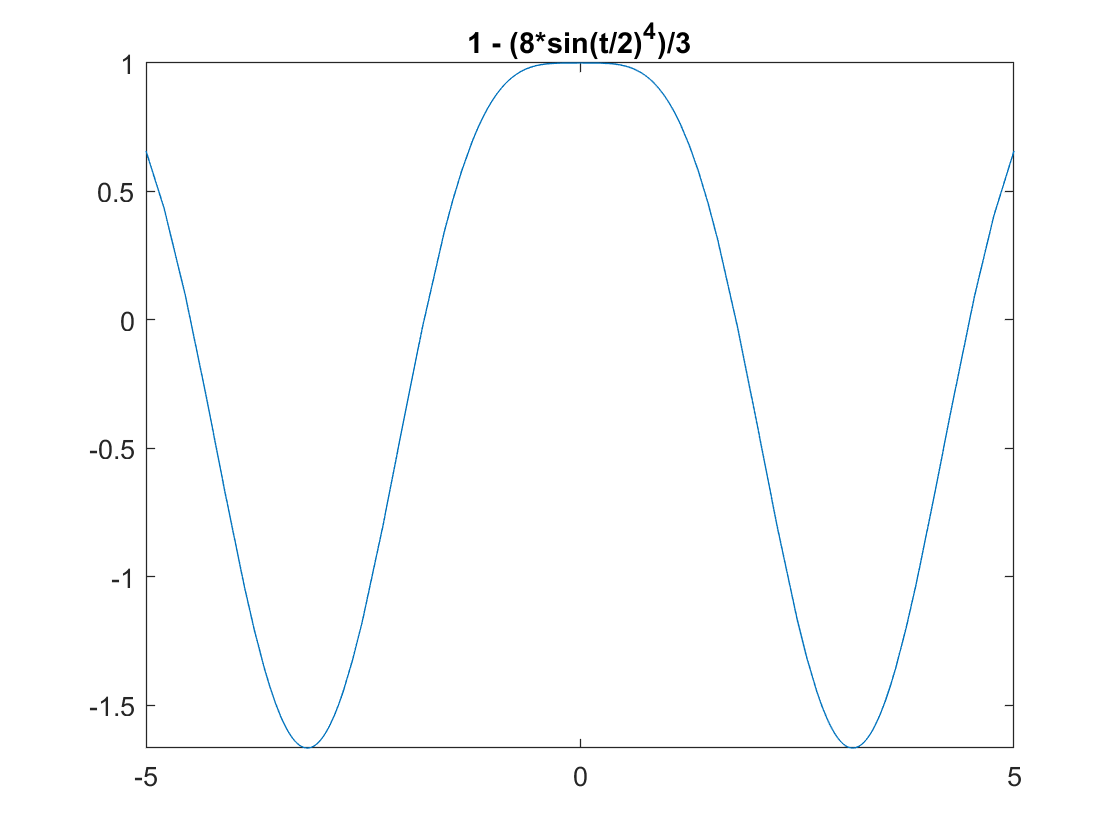
\[\frac{d^2y}{dt^2} = cos(2t)- y\]with initial conditions
\[y(0) = 1\] \[y'(0) = 0\]Follows the same pattern as the other one but defining one more condition.
syms y(t)
Dy = diff(y,t)
ode = diff(y,t,2) == cos(2*t) - y
cond1 = y(0) == 1
cond2 = Dy(0) == 0
ySol(t) = dsolve(ode,[cond1 cond2])
Find more about solving ODEs analytically