CHOs
IMPORTANT Some of these functions require the Symbolic Math Toolbox to work. Make sure it is installed before trying to use them.
The following example will show how to solve a CHO problem alongside matlab. This is complex and requires a good understanding of the physical system.
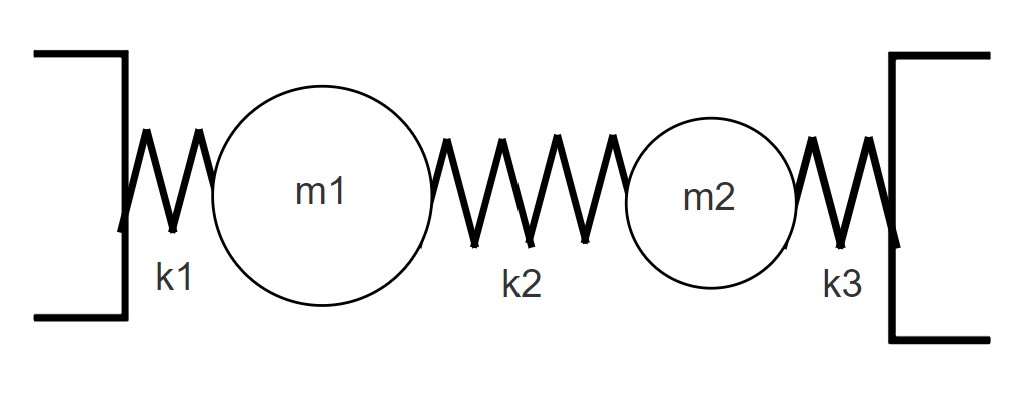
Taking the right as the positive direction we can determine the equations of motion for these two masses.
\[m_1\ddot{x_1} = k_2(x_2 - x_1) - x_1k_1\] \[m_2\ddot{x_2} = k_2(x_1 - x_2) - x_2k_3\]Divide by the masses and then construct a matrix:
\[\begin{bmatrix} \ddot{x_1} \\ \ddot{x_2} \end{bmatrix} = \begin{bmatrix} \frac{-(k_2 + k_1)}{m_1} & \frac{k_2}{m_1} \\ \frac{k_2}{m_2} & \frac{-(k_2+k_3)}{m_2} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\]We can define all these elements as symbolic variables in matlab and find it’s eigenvalues.
syms k m
k1 = k
k2 = 2*k
k3 = 3*k
m1 = 3*m
m2 = m
A = [-(k2 + k1)/(m1), k2/m1 ; k2/m2, -(k2 + k3)/(m2)]
[v ,d] = eig(A)
The eigenvalues result to be :
\[\lambda_1 = \frac{k(4\sqrt{3} - 9)}{3m}\] \[\lambda_2 = -\frac{k(4\sqrt{3} + 9)}{3m}\]And their natural frequencies are given by:
\[\lambda_1 = -\omega_1^2\] \[\lambda_2 = -\omega_2^2\]Therefore:
\[\omega_1 = \sqrt{-\frac{k(4\sqrt{3} - 9)}{3m}}\] \[\omega_2 = \sqrt{\frac{k(4\sqrt{3} + 9)}{3m}}\]And their respective eigenvectors tell us how they move
\[v_1 = (2.155,1) (in phase)\] \[v_2 = (-0.155, 1) (antiphase)\]