Fourier series
IMPORTANT Some of these functions require the Symbolic Math Toolbox to work. Make sure it is installed before trying to use them.
The following example will show how to solve a fourier series question using Matlab
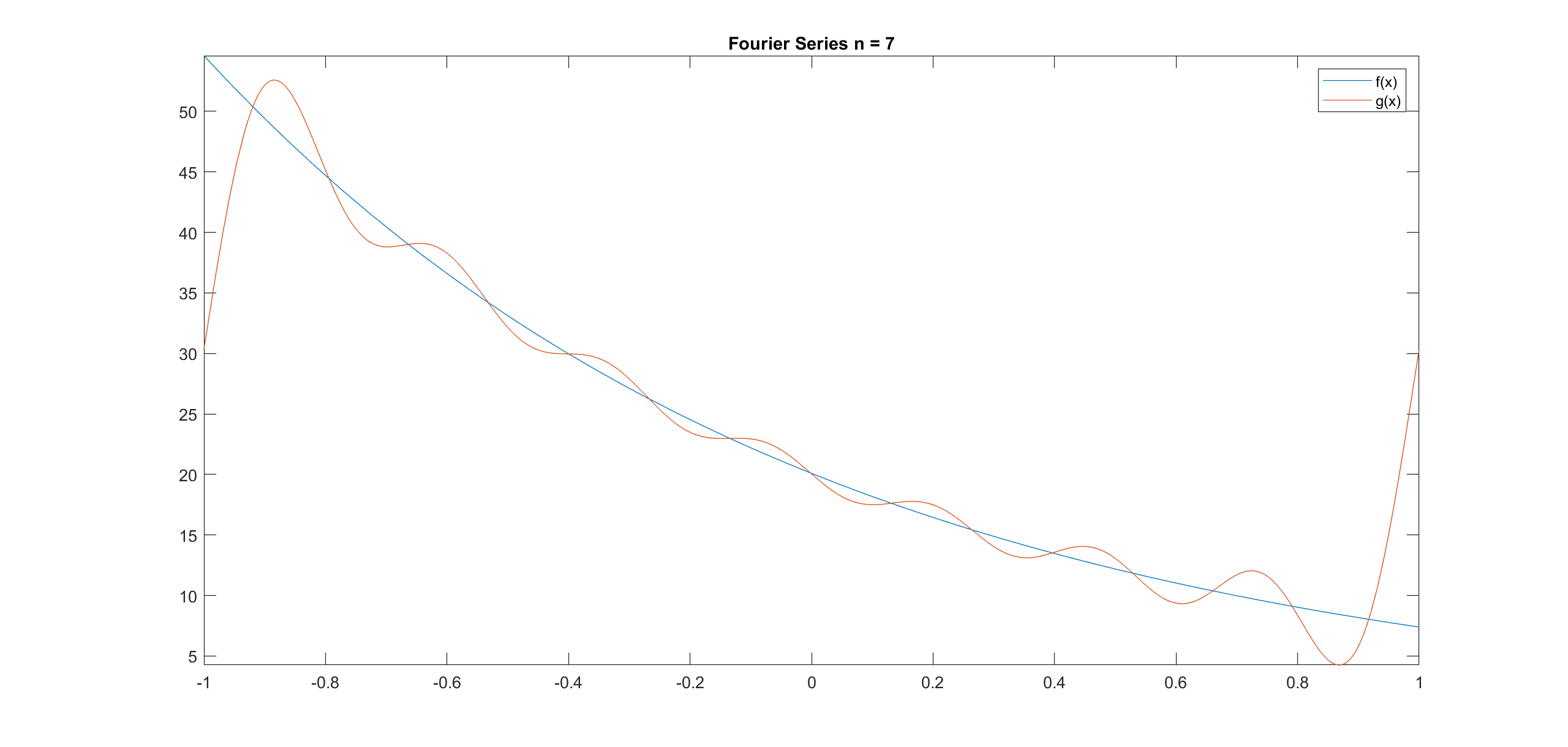
Compute the Fourier Series of the following function in the range [-1 1].
\[f(x) = e^{-x + 3}\]For a Fourier Series:
\[a_0 = \frac{1}{L} \int_{-L}^{L} f(x) dx\] \[a_n = \frac{1}{L} \int_{-L}^{L} f(x)\cos(\frac{n\pi x}{L})dx\] \[b_n = \frac{1}{L} \int_{-L}^{L} f(x)\sin(\frac{n\pi x}{L})dx\] \[g(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(\frac{n\pi x}{L}) + \sum_{n=1}^{\infty} b_n \sin(\frac{n\pi x}{L})\]- First we need to declare our symbolic variables, the function we want to analyse and within what range.
syms n x f = exp(-x+3); range = [-1 1]; nmax = 7; - Then we declare a0 in terms of f and the range, the symbolic integration is done using the int() function.
a0 = 1/range(1,2)*int(f,range); - an and bn are special because they have to be declared as functions of n not just symbolic expressions. This is because later on the summation step we need to be able to input different values of n to the an and bn expressions.
an = @(n) 1/range(1,2)*int(f*cos(pi*n*x/range(1,2)),range); bn = @(n) 1/range(1,2)*int(f*sin(pi*n*x/range(1,2)),range); - Finally we declared g and construct the summation statements using the symsum() function.
g = a0/2 + symsum(an(n)*cos(n*pi*x/range(1,2)),n,1,nmax) + symsum(bn(n)*sin(pi*n*x/range(1,2)),n,1,nmax)The summation on the example goes from n = 1 to n = 7. Plotting it it would look like: