MVC
IMPORTANT Some of these functions require the Symbolic Math Toolbox to work. Make sure it is installed before trying to use them.
MVC operations
-
diff(f(x),x,n) computes the nth derivative of f(x) which is a symbolic expression with respect to x. If n is omitted it will be the first order derivative. Full documentation
syms x; f = x^3-4*x; diff(f,x,2) -
int(expr,var,a,b) computes the definite integral of symbolic expr with respect to var from a to b. If a and b are omitted then it will return a symbolic expression of the indefinite integral. Full documentation
syms x; expr = sin(x) - x^4; int(expr,x) - divergence(V,vars) computes the divergence of a vector field V with respect to the variables vars. V and vars are both row matrices and should have the same size. Full Documentation
syms x y z V = [x^2, 3*y + y^2, z^3]; vars = [x y z]; divergence(V,vars) - curl(V,vars) computes the curl of a vector field with respect to the variables vars. V and vars are both row matrices and should have the same size. Full Documentation
syms x y z V = [x^2*y*z, 3*y + y^2 - z, x*z^3]; vars = [x y z] curl(V,vars) - gradient(f,vars) computes the gradient of a function f with respect to the variables vars. Where vars is a row matrix. Full Documentation
syms x y z f = 2*x^3 + sin(y)*cos(z) vars = [x y z] gradient(f,vars) - laplacian(f,vars) computes the laplacian of a function f with respect to the variables vars. Where vars is a row matrix. Full Documentation
syms x y z f = cos(x)*y - z^3; vars = [x y z]; laplacian(f,vars)
Plotting
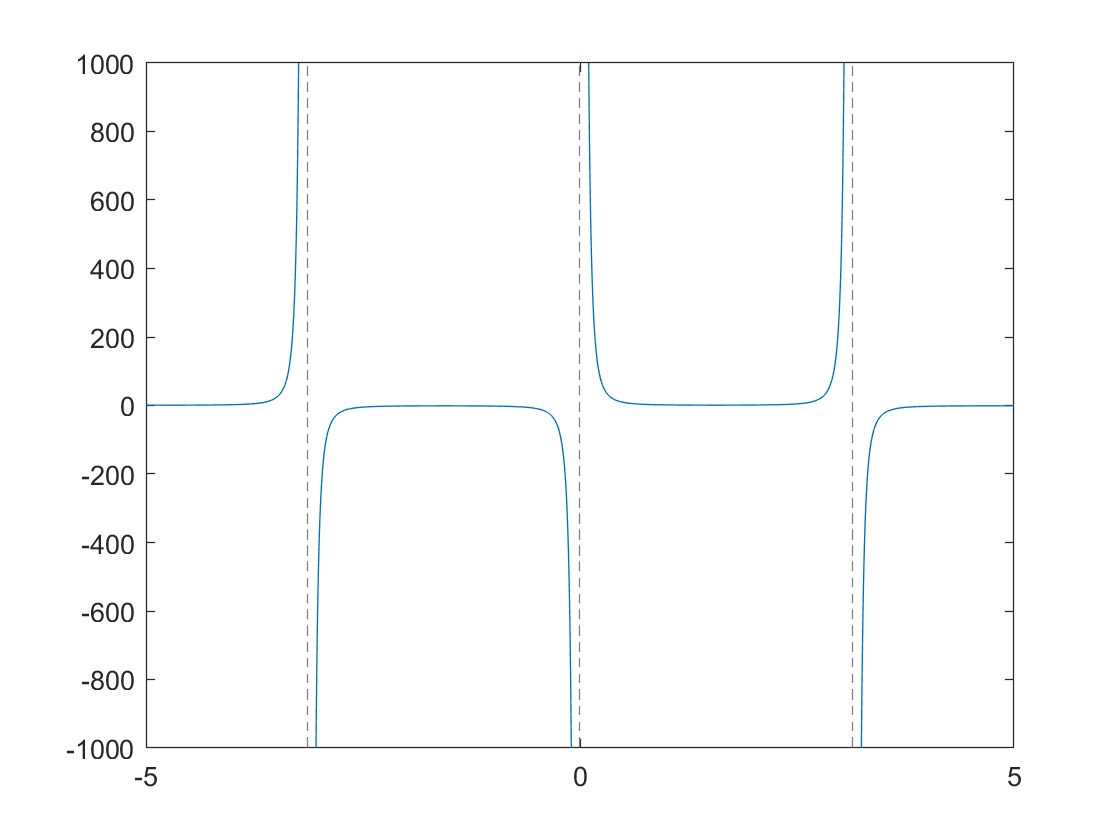
- fplot(f(x),Range) similar to plot() but instead it takes a symbolic function and a range as [xmin xmax] to plot the function through. If the Range argument is omitted the range is [-5 to 5]. Full Documentation
f = @(x) sin(x)^-3; fplot(f)
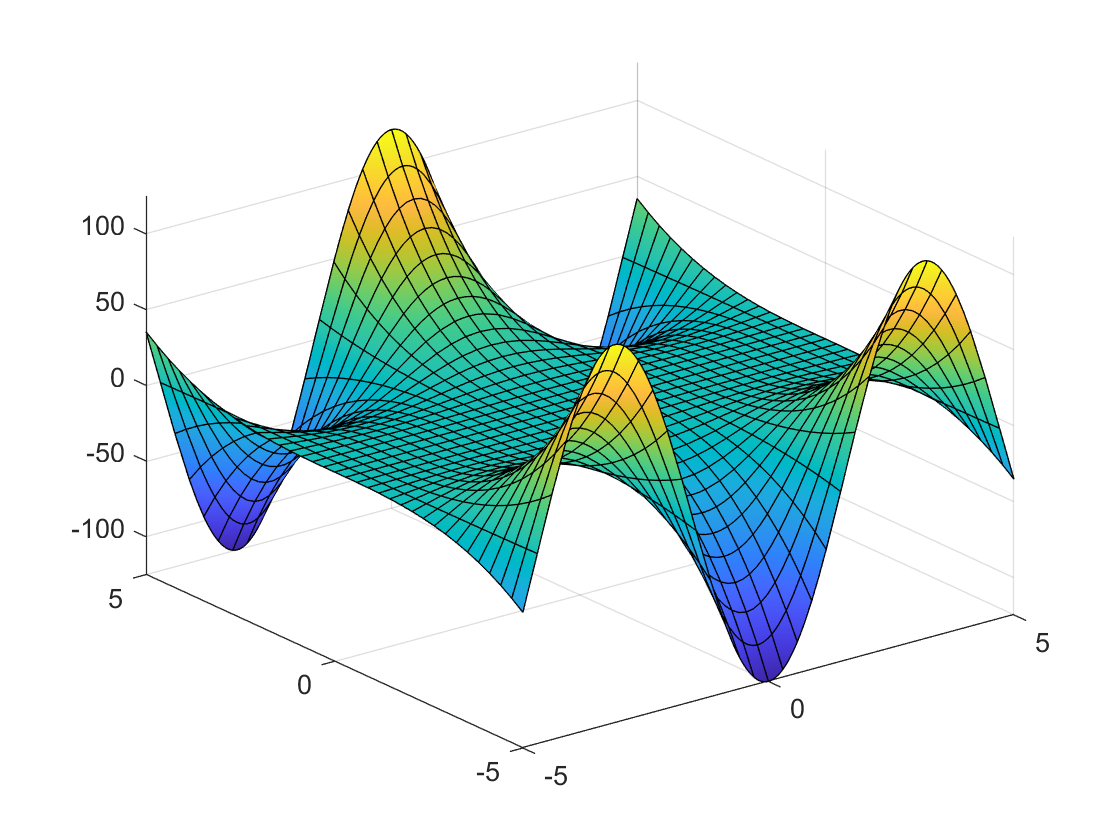
- fsurf(f(x,y),xyinterval) generates a 3D plot of a symbolic function of 2 variables, the second argument is a matrix that contains the following values [xmin xmax ymin ymax]. By default it’s interval is [-5 to 5] for both x and y. Full Documentation
f = @(x,y) cos(x)*y^3; fsurf(f)