Linear Transformations

<= Back to the Cheatsheet

IMPORTANT You will need to have a WolframAlpha Pro account to use Wolfram effectively.

Linear transformations rely very heavily on matrices. For example, calculating the change in size due to a transformation using the determinant, and obtaining the transformation required to undo initial transformation by means of the inverse. You can use a matrix-vector multiplication to obtain the resulting vector after applying a linear transformation.

Rotation

You can ask Wolfram to rotate shapes and points for you.

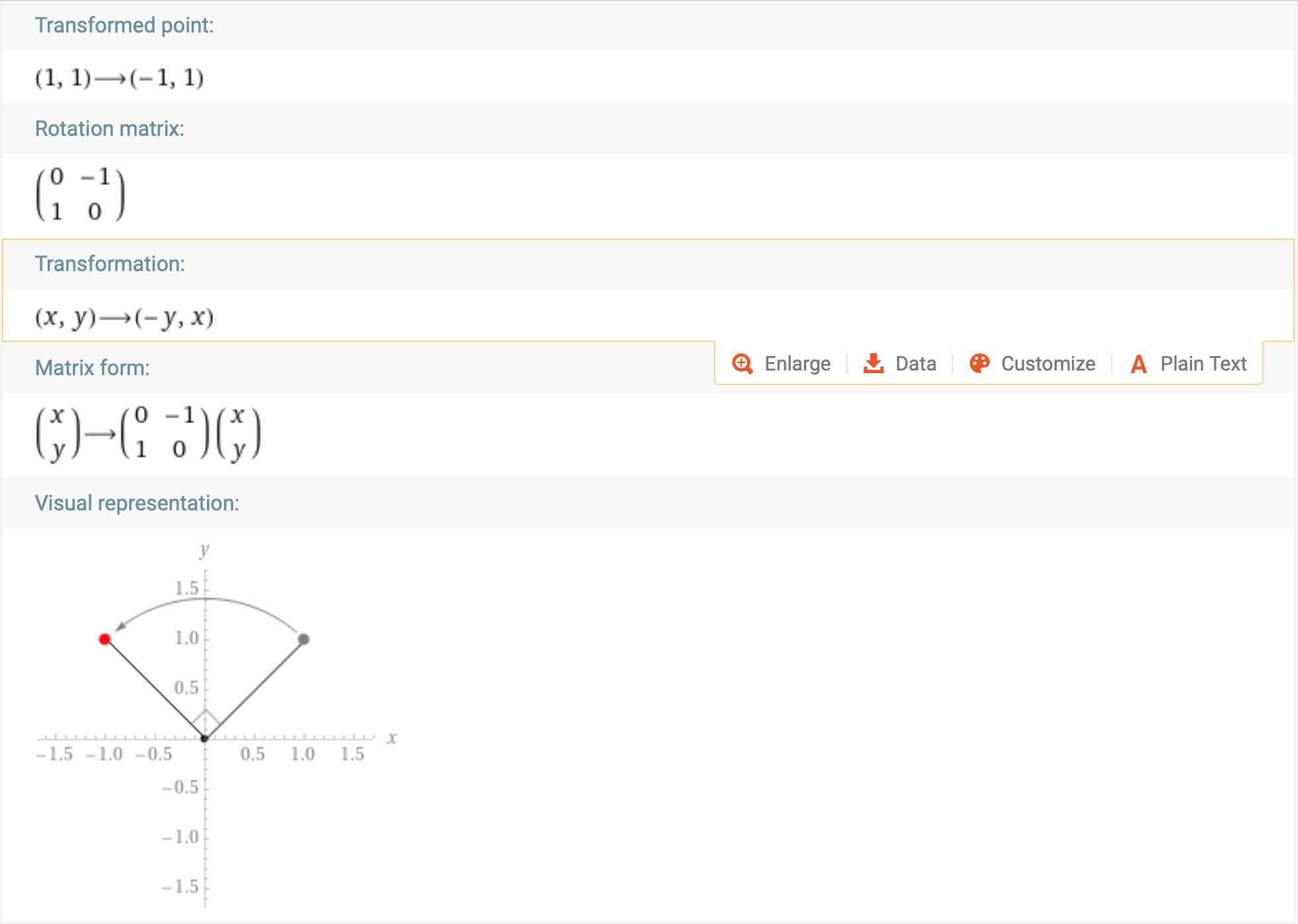
Shears

In order to get Wolfram to perform shears, you do need to give it the shear matrix, defining your shear factor a to adjust the size of the shear, like this.

Scaling

Scaling works in a similar way, where you need to specify your scale factors.

Solution of a homogeneous linear system

Here is an example of the null space (kernel), and a non-homogeneous system. You can visualize the solution on cartesian axes.