Vectors, Sheet #2
Learning Targets
- Add and subtract vectors
- Find the modulus of a vector
- Find the unit vector
- Calculate the scalar product
- Use $\cos{\theta} = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$
- Use the cross product
- Use basis vectors
- Find the cartesian and vector equations for a plane
- Find the minimum distance between vectors
Additional Resources
Tutorials
- Linear Algebra Playlist : Vectors and matrices, going on to eigens, very good for intuition. Don’t panic if you don’t understand all of it, you haven’t been taught it all!
- Skew Vectors Tutorial : Skew vectors done step by step - good for understanding.
Software
- Skew Vectors Calculator : Circumvent any manual calculation by having a computer do it for you - make sure you understand how it works before skipping to the end though!
Problem sheet
Skill Building Questions
Problem 1.
Consider the three vectors $\vec{a}= (2,1,0)$, $\vec{b}= (-1,2,3)$, and $\vec{c}= (1,2,1)$. Calculate the following:
(a) $\vec{a}+\vec{b}$
(b) $2\vec{a}-\vec{b}$
(c) $\vec{a}\circ\vec{b}\circ \vec{c}$
(d) $| \vec{c} |$
(e) Find the unit vector in direction of $\vec{c}$.
(f) Find the volume of the parallelepiped described by the vectors $\vec{a}, \vec{b}$ and $\vec{c}$ (hint: Use Triple scalar product).
Problem 2.
Scalar product calculation.
(a) Let $\vec{a} = \hat{i}+2\hat{j} $ and $ \vec{b} =2\hat{i}+\hat{j}. $ Is $ | \vec{a} | = | \vec{b} |?$ Are the vectors $\vec{a}$ and $\vec{b}$ equal ?
(b) Find the vector from point $P(2, 3, 0)$ to $Q(-1, -2, -4)$:
(c) Find the angle $\theta$ between the vectors $\vec{a} = \hat{i}+\hat{j}-\hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+\hat{k}$ :
(d) If $\vec{a} = 5\hat{i}-\hat{j}-3\hat{k}$ and $\vec{b} = \hat{i}+3\hat{j}-5\hat{k}$, then show that the vectors $\vec{a}+\vec{b}$ and $\vec{a}-\vec{b}$ are perpendicular.
(e) Show the points $A(-2\vec{i}+3\vec{j}+5\vec{k})$, $B(\vec{i}+2\vec{j}+3\vec{k})$, and $C(7\vec{i}-\vec{k})$ are collinear (They lie on the same straight line).
Scalar Product Visualization
To help with intuition when answering these questions, here is a visualization built in Manim. You can play around with it here!
Problem 3.
Cross product calculation.
(a) Find $|\vec{a}\times\vec{b}|,$ if $\vec{a}=2\vec{i}+\vec{j}+3\vec{k}$ and $\vec{b}=3\vec{i}+5\vec{j}-2\vec{k}$
(b) Find the area of a triangle having the points $A(1,1,1)$, $B(1,2,3)$ and $C(2,3,1)$ as its vertices
(c) Find a unit vector perpendicular to each of the vectors $(\vec{a}+\vec{b})$ and $(\vec{a}-\vec{b})$, where $\vec{a} = \hat{i}+\hat{j}+\hat{k} $, $\vec{b}= \hat{i}+2\hat{j}+3\hat{k}$.
(d) Find the area of a parallelogram which adjacent sides are given by the vectors $\vec{a}= 3\hat{i}+\hat{j}+4\hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+\hat{k}$
Cross Product Visualization
To help with intuition when answering these questions, here is a visualization built in Manim. You can play around with it here!
Problem 4.
Analytical geometry calculation.
(a) Find the equation for a plane through the point $(0,1,-7)$ which is perpendicular to the vector $(4,-1,6)$.
(b) Find the equation for a plane through the points $A=(0,1,-7),B=(3,1,-9), $ and $C=(0,-5,-8)$.
(c) Find the angle $\theta$ between two lines in the x, y-plane, given by the equations: $3x-4y+1=0$ and $2x+y-5=0$
(d) Let ABC be a triangle in the x, y-plane, with the vertices at the points $A = (2,-1)$, $B=(4,4)$ and $C=(9,7)$. Find the distance from point A normal to line BC:
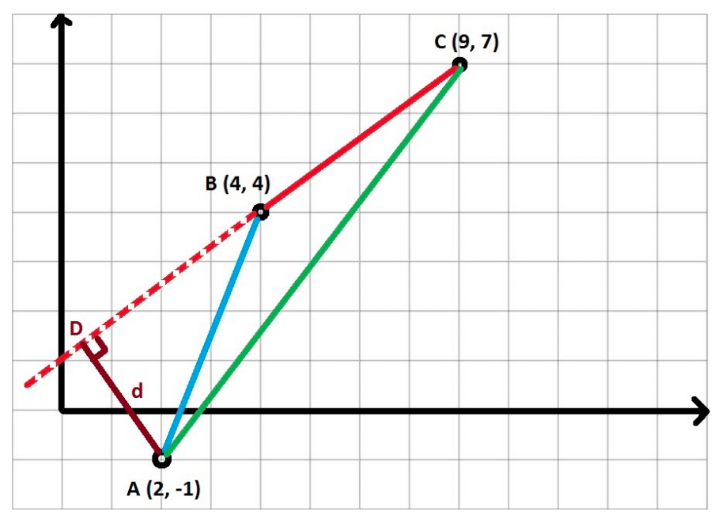 Find the equation of line BC:
$$ \text{Gradient} = C - B =
\begin{bmatrix}
5\\\\
3
\end{bmatrix}$$
$$ \therefore BC =
\begin{bmatrix}
4 \\\\
4
\end{bmatrix} + \lambda
\begin{bmatrix}
5 \\\\
3
\end{bmatrix}$$
The point D is the perpendicular intersection between line BC and A, where D can be expressed as a point on the line BC with a value of lambda to be found:
$$D =
\begin{bmatrix}
4 + 5\lambda \\\\
4 + 3\lambda
\end{bmatrix}$$
Therefore, we can form an equation for line AD:
$$ \text{Gradient} = A - D =
\begin{bmatrix}
-2 - 5\lambda\\\\
-5 - 3\lambda
\end{bmatrix}$$
$$\therefore AD =
\begin{bmatrix}
2 \\\\
-1
\end{bmatrix} + \mu
\begin{bmatrix}
-2 - 5\lambda\\\\
-5 - 3\lambda
\end{bmatrix} $$
As we know that lines BC and AD are perpendicular, the dot product of their gradients will be equal to 0:
$$(-10 - 25\lambda) + (-15 - 9\lambda) = 0$$
$$\lambda = \frac{-25}{34}$$
We can use the AD gradient with this value of lambda to find the distance between A and D, d:
$$d^2 = (-2 - 5\lambda)^2 + (-5 - 3\lambda)^2$$
$$\boxed{ { d } ={\frac{19}{\sqrt{34}}}}$$
Find the equation of line BC:
$$ \text{Gradient} = C - B =
\begin{bmatrix}
5\\\\
3
\end{bmatrix}$$
$$ \therefore BC =
\begin{bmatrix}
4 \\\\
4
\end{bmatrix} + \lambda
\begin{bmatrix}
5 \\\\
3
\end{bmatrix}$$
The point D is the perpendicular intersection between line BC and A, where D can be expressed as a point on the line BC with a value of lambda to be found:
$$D =
\begin{bmatrix}
4 + 5\lambda \\\\
4 + 3\lambda
\end{bmatrix}$$
Therefore, we can form an equation for line AD:
$$ \text{Gradient} = A - D =
\begin{bmatrix}
-2 - 5\lambda\\\\
-5 - 3\lambda
\end{bmatrix}$$
$$\therefore AD =
\begin{bmatrix}
2 \\\\
-1
\end{bmatrix} + \mu
\begin{bmatrix}
-2 - 5\lambda\\\\
-5 - 3\lambda
\end{bmatrix} $$
As we know that lines BC and AD are perpendicular, the dot product of their gradients will be equal to 0:
$$(-10 - 25\lambda) + (-15 - 9\lambda) = 0$$
$$\lambda = \frac{-25}{34}$$
We can use the AD gradient with this value of lambda to find the distance between A and D, d:
$$d^2 = (-2 - 5\lambda)^2 + (-5 - 3\lambda)^2$$
$$\boxed{ { d } ={\frac{19}{\sqrt{34}}}}$$(e) Find the unit vector in the direction of the sum of the vectors, $\vec{a}=2\vec{i}+2\vec{j}-5\vec{k}$ and $\vec{b}=2\vec{i}+\vec{j}+3\vec{k}$.
Problem 5.
Show that the points $A = (2\hat{i},-\hat{j},\hat{k})$, $B = (\hat{i},-3\hat{j},-5\hat{k})$ and, $C = (3\hat{i},-4\hat{j},-4\hat{k})$ are the vertices of a right angled triangle.
Problem 6.
Use the scalar triple product to show that the vectors $a=2i+3j+k, b=i-j, c=7i+3j+2k$, are coplanar, that is, they lie in the same plane.
Volume = $|a||\cos\phi||b\times c|=\vec{a}\cdot(\vec{b}\times \vec{c})$ Volume=$\vec{a}\cdot(\vec{b}\times\vec{c})=(2,3,1)\cdot \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 0 \\ 7 & 3 & 2 \\ \end{vmatrix}=(2,3,1)\big(\begin{vmatrix} -1&0\\ 3&2\\ \end{vmatrix}\hat{i}-\begin{vmatrix} 1&0\\ 7&2\\ \end{vmatrix}\hat{j}+\begin{vmatrix} 1&-1\\ 7&3\\ \end{vmatrix}\hat{k}\big)$
Volume=$(2,3,1)(-2,-2,10)=-4-6+10=0$ Therefore, the volume of the parallelepiped formed by vector a,b,c is 0. $\boxed{\textrm{This means } \vec{a},\vec{b}, \textrm{ and } \vec{c} \textrm{ are coplanar.}}$
Problem 7.
Given the basis vectors $\vec{a} = 2\hat{i} - 3\hat{j}$ and $\vec{b} = \hat{i} + 2\hat{j}$, what is the vector $(4, -9)$ equivalent to?
$4\vec{a} = 8\hat{i} - 12\hat{j}$
$-9\vec{b} = -9\hat{i} - 18\hat{j}$
$(4, -9) = (8-9)\hat{i} + (-12 - 18)\hat{j}$
$(4, -9) = \boxed{-\hat{i} -30\hat{j}}$
Problem 8.
The lines $l_1$ and $l_2$ have equations $\begin{pmatrix}
1, \
0, \
0 \
\end{pmatrix} + \lambda\begin{pmatrix}
0, \
1, \
1 \
\end{pmatrix} $ and $\begin{pmatrix}
-1, \
3, \
-1 \
\end{pmatrix} + \mu\begin{pmatrix}
2, \
-1, \
-1 \
\end{pmatrix} $ respectively, where $\lambda$ and $\mu$ are scalars.
Find the shortest distance, $d$, between these two lines.
Let $A$ and $B$ be general points on $l_1$ and $l_2$ respectively.
$A = \begin{pmatrix} 1 \\\\ \lambda \\\\ \lambda \\\\ \end{pmatrix}$ and $B = \begin{pmatrix} -1 + 2\mu \\\\ 3 - \mu \\\\ -1 - \mu \\\\ \end{pmatrix}$
$\vec{AB} = \begin{pmatrix} -1 + 2\mu \\\\ 3 - \mu \\\\ -1 - \mu \\\\ \end{pmatrix} - \begin{pmatrix} 1 \\\\ \lambda \\\\ \lambda \\\\ \end{pmatrix} = \begin{pmatrix} -2 + 2\mu \\\\ 3 - \mu -\lambda \\\\ -1 - \mu - \lambda \\\\ \end{pmatrix} $
As $\vec{AB}$ is perpendicular to both $l_1$ and $l_2$, the scalar product of the direction vectors of the lines is zero. This can be used to generate linear equations in $\lambda$ and $\mu$.
$\vec{AB}$ is perpendicular to $l_1$:
$\begin{pmatrix} -2 + 2\mu \\\\ 3 - \mu -\lambda \\\\ -1 - \mu - \lambda \\\\ \end{pmatrix}\cdot\begin{pmatrix} 0 \\\\ 1 \\\\ 1 - \mu - \lambda \\\\ \end{pmatrix} = 0$
$3 - \mu - \lambda - 1 - \mu - \lambda = 0 \Rightarrow\quad 2 - 2\mu - 2\lambda = 0\quad (1)$
$\vec{AB}$ is perpendicular to $l_2$:
$\begin{pmatrix} -2 + 2\mu \\\\ 3 - \mu -\lambda \\\\ -1 - \mu - \lambda \\\\ \end{pmatrix}\cdot\begin{pmatrix} 2 \\\\ -1 \\\\ -1 - \mu - \lambda \\\\ \end{pmatrix} = 0$
$ -4 + 4\mu - 3 + \mu + \lambda + 1 + \mu + \lambda = 0 \Rightarrow\quad -6 + 6\mu + 2\lambda = 0\quad (2)$
Rearranging equation $(1)$ gives $\lambda = 1 - \mu$. This can be substituted into equation $(2)$.
$ -6 + 6\mu +2(1 - \mu) = 0 \Rightarrow\quad -4 + 4\mu = 0 \Rightarrow\quad \mu = 1$
Therefore, $\lambda = 1 - 1 = 0 $
$\vec{AB} = \begin{pmatrix} -2 + 2(1) \\\\ 3 - 1 - 0 \\\\ -1 - 1 - 0 \\\\ \end{pmatrix} = \begin{pmatrix} 0 \\\\ 2 \\\\ -2 \\\\ \end{pmatrix} $
The length of $\vec{AB}$ is the shortest distance between the lines.
Shortest distance, $d = |\vec{AB}| = \sqrt{0^2 + 2^2 + (-2)^2} = \boxed{2\sqrt{2}}$
Method 2 (The quick way):
Method 1 can be replaced by a short-cut equation:
For two lines given in the form $l_1 = \vec{a_1} + \lambda\vec{b_1}$ and $l_2 = \vec{a_2} + \mu\vec{b_2}$, $ d = \frac{|(\vec{a_2} - \vec{a_1})\cdot(\vec{b_1}\times\vec{b_2})|}{|(\vec{b_1}\times\vec{b_2})|}$
$\vec{a_2} - \vec{a_1} = \begin{pmatrix} -1 \\\\ 3 \\\\ -1 \\\\ \end{pmatrix} - \begin{pmatrix} 1 \\\\ 0 \\\\ 0 \\\\ \end{pmatrix} = \begin{pmatrix} -2 \\\\ 3 \\\\ -1 \\\\ \end{pmatrix}$
$ \vec{b_1}\times\vec{b_2} = \begin{pmatrix} 0 \\\\ 1 \\\\ 1 \\\\ \end{pmatrix}\times\begin{pmatrix} 2 \\\\ -1 \\\\ -1 \\\\ \end{pmatrix} = \begin{pmatrix} 0 \\\\ 2 \\\\ -2 \\\\ \end{pmatrix} $
$ |\vec{b_1}\times\vec{b_2}| = \sqrt{0^2 + 2^2 + (-2)^2} = 2\sqrt{2} $
$ (\vec{a_2} - \vec{a_1})\cdot(\vec{b_1}\times\vec{b_2}) = \begin{pmatrix} -2 \\\\ 3 \\\\ -1 \\\\ \end{pmatrix}\cdot\begin{pmatrix} 0 \\\\ 2 \\\\ -2 \\\\ \end{pmatrix} = 0 + 6 + 2 = 8 $
Finally, $d = \frac{8}{2\sqrt{2}} = \boxed{2\sqrt{2}}$
Problem 9.
The locations of a pair of long straight pipes are specified using Cartesian co-ordinates as follows:
- Pipe $A$: diameter 0.8; axis through points $P (2, 5, 3)$ and $Q (7, 10, 8)$.
- Pipe $B$ diameter 1.0; axis through points $R (0, 6, 3)$ and $S (−12, 0, 9)$.
Do the pipes need re-aligning to avoid intersection? (Assume the origin position O is (0,0,0)).
Hence, $\boxed{\text{the pipes do NOT need re-aligning to avoid intersection.}}$
Exam Style Questions
Problem 10.
The diagram below shows a cuboid $OABCDEFG$ with coordinates as shown. The point P has coordinates $(4,2,0)$.
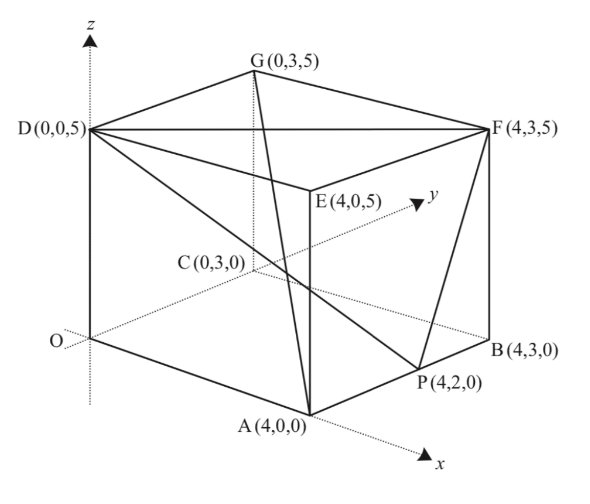
(a) Find the length of the diagonal $AG$
(b) Show that the vector $\textbf{n} = 15\textbf{i} - 20\textbf{j} +4\textbf{k}$ is normal to the plane $DPF$. Hence find the cartesian equation of this plane.
$\overrightarrow{DF} = 4\textbf{i} +3\textbf{j} \space \text{(or }\ \overrightarrow{PF} = \textbf{j} + 5\textbf{k})$
The scalar product should equal $0$ if the vector $\textbf{n}$ is perpendicular to the plane.
$\textbf{n} \cdot \overrightarrow{DP} = 15 \times 4 - 20 \times 2 + 4 \times (-5) = 0 $
$\textbf{n} \cdot \overrightarrow{DF} = 15 \times 4 - 20 \times 3 = 0 $
$\text{(or } \textbf{n} \cdot{PF} = -20 \times 1 + 4 \times 5 = 0)$
$\textbf{r} \cdot \textbf{n} = \textbf{a} \cdot \textbf{n} \Rightarrow\boxed{15x - 20 y + 4z = 20}$
(c) The diagonal $AG$ intersects the plane $DPF$ at $Q$. Write down a vector equation of the line $AG$. Hence find the coordinates of the point $Q$, and the ratio $AQ:QG$.
$\textbf{r} = (4 - 4\lambda)\textbf{i} + 3\lambda\textbf{j} + 5\lambda\textbf{k}$
Substitute the components of the vector equation of the line AG into the equation for the plane $DPF$.
$15(4 - 4 \lambda) - 20 (3 \lambda) + 4 (5 \lambda) = 20 \Rightarrow 40 = 100 \lambda, \lambda = 0.4$
$Q$ is $(2.4, 1.2, 2)$
$\overrightarrow{AQ} = (-1.6, 1.2, 2)$ and $\overrightarrow{QG} = (-2.4, 1.8, 3)$
$\frac{-1.6}{-2.4} = \frac{1.2}{1.8} = \frac{2}{3} $
Therefore, $\boxed{AQ : QG = 2 : 3}$
(d) Find the acute angle between the line $AG$ and the plane $DPF$.
$ cos\theta = \frac{(-4\times15) + (3\times-20)+(5\times4)}{\sqrt{50}\sqrt{641}}$
$\theta = 56.0$ or $124.0$
$\boxed{\text{Angle between line and plane } = 34.0^\circ}$
Problem 11.
A mahi-mahi fish, initially located at $(-4,3,-2)km$, begins to swim towards a coral reef with velocity
$\begin{pmatrix}
1,
7,
-6
\end{pmatrix} \text{km/h}$.
(a) What is the speed of the fish in km/h to 2 decimal places?
(b) A deep sea buoy floats on the surface of the water at location $(8,6,0)km$ and is attached by a chain to an anchor that sits on the sea bed (the buoy does not move from its given position at sea-level).
The vector $\begin{pmatrix}
1,
-1,
-4
\end{pmatrix} $ describes the direction of the anchor from the buoy. The ocean is $10$km deep. How long is the anchor chain to 2 decimal places?
$\Rightarrow$ Chain length $= \left| \begin{pmatrix} 2.5\\-2.5\\-10 \end{pmatrix} \right| = \sqrt{2.5^2 + (-2.5)^2 + (-10)^2} = \boxed{10.61 km}$
(c) What is the minimum distance from the buoy to the mahi-mahi fish to 2 decimal places?
$\vec{s} = \begin{pmatrix} -4\\3\\-2 \end{pmatrix} + t \begin{pmatrix} 1\\7\\-6 \end{pmatrix} = \begin{pmatrix} -4+t\\3+7t\\-2-6t \end{pmatrix} $
When the fish is closest to the buoy, the velocity vector of the fish $\vec{v}$ will be perpendicular to the vector from the fish to the buoy, which is represented by $(\vec{b} - \vec{s})$.
$\vec{v} \cdot (\vec{b} - \vec{s}) = 0 = \begin{pmatrix} 1\\7\\-6 \end{pmatrix} \cdotp \begin{pmatrix} 8 -(-4+t)\\6-(3+7t)\\0-(-2-6t) \end{pmatrix} = 1(12-t) + 7(3-7t) - 6(2+6t) \\ = 21 - 86t = 0 \Rightarrow{t = \frac{21}{86}}$
The minimum distance between the fish and the buoy is the length of the vector $(\vec{b} - \vec{s})$.
$ |(\vec{b}-\vec{s})| = \sqrt{(12-t)^2 + (3-7t)^2 + (2+6t)^2} = \boxed{12.32 km} $
Extension Questions
Problem 12.
Prove any given three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ satisfy the relationship \((\vec{a}+\vec{b})+\vec{c} = \vec{a} + (\vec{b} + \vec{c})\)
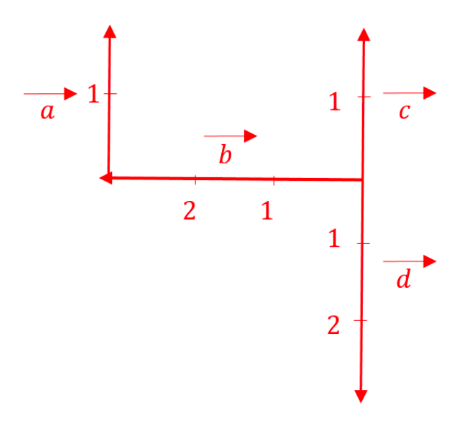 From the graph,
$$\vec{a}+\vec{b}=\vec{PQ}+\vec{QR}=\vec{PR}$$
$$\vec{b}+\vec{c}=\vec{QR}+\vec{RS}=\vec{QS}$$
$$(\vec{a}+\vec{b})+\vec{c}=\vec{PR}+\vec{RS}=\vec{PS}$$
$$\vec{a}+(\vec{b}+\vec{c})=\vec{PQ}+\vec{QS}=\vec{PS}$$
Therefore
$$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$$
From the graph,
$$\vec{a}+\vec{b}=\vec{PQ}+\vec{QR}=\vec{PR}$$
$$\vec{b}+\vec{c}=\vec{QR}+\vec{RS}=\vec{QS}$$
$$(\vec{a}+\vec{b})+\vec{c}=\vec{PR}+\vec{RS}=\vec{PS}$$
$$\vec{a}+(\vec{b}+\vec{c})=\vec{PQ}+\vec{QS}=\vec{PS}$$
Therefore
$$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$$
Problem 13.
The points $A$, $B$ and $C$ have position vectors $(-2, -3,0)$, $(-1, -1, 3)$ and $(1, 1, 1)$ respectively. Find the centre and radius of the circle that passes through all three points.
Therefore, $\textbf{r} = \begin{pmatrix} 1\\1\\1 \end{pmatrix} + \lambda\begin{pmatrix} 2\\2\\-2 \end{pmatrix} + \mu\begin{pmatrix} 3\\4\\1 \end{pmatrix}$
$\overrightarrow{AX}$, $\overrightarrow{BX}$ and $\overrightarrow{CX}$ are radii of the circle which passes through $A$, $B$ and $C$.
$|\overrightarrow{AX}|^2 = |\overrightarrow{CX}|^2$
$(3+(2\lambda+3\mu))^2 + (4+(2\lambda=4\mu))^2 + (1+(-2\lambda+\mu))^2 = (2\lambda +3\mu)^2 + (2\lambda + 4\mu)^2 + (-2\lambda+\mu)^2 $
$ 26 + 6(2\lambda + 3\mu) + 8(2\lambda + 4\mu) + 2(-2\lambda + \mu) = 0 $
$ 26 + 24\lambda + 52\mu = 0,\quad (1)$
$ |\overrightarrow{BX}|^2 = |\overrightarrow{CX}|^2$
$ (2 + (2\lambda+3\mu))^2 + (2 + (2\lambda + 4\mu))^2 + (-2 + (-2\lambda + \mu))^2 = (2\lambda +3\mu)^2 + (2\lambda + 4\mu)^2 + (-2\lambda+\mu)^2$
$ 12 + 4(2\lambda + 3\mu) + 4(2\lambda + 4\mu) - 4(-2\lambda + \mu) = 0$
$ 12 + 24\lambda + 24\mu = 0,\quad (2)$
Solving equations $(1)$ and $(2)$ simultaneously,
$(1) - (2): 14 + 28\mu = 0 \Rightarrow \mu = -\frac{1}{2}$
Substituting $\mu = -\frac{1}{2}$ into $(2)$:
$ 12 + 24\lambda + 24(-\frac{1}{2}) = 0$
$ 24\lambda = 0 \Rightarrow\quad \lambda = 0 $
Therefore, $\textbf{r} = \begin{pmatrix} 1\\1\\1 \end{pmatrix} + -\frac{1}{2}\begin{pmatrix} 3\\4\\1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2}\\-1\\\frac{1}{2} \end{pmatrix}$
Therefore, the coordinates of the centre of the circle are $\boxed{(-\frac{1}{2}, -1, -\frac{1}{2})}$.
The point X is equidistant to each point $A$, $B$ and $C$ (since $A$, $B$ and $C$ lie on circumference of circle centre X).
Considering point $C$, the radius $r$ is given by:
$ r = |\overrightarrow{CX}| = \sqrt{(1-(-\frac{1}{2}))^2 + (1-(-1))^2 + (1 - \frac{1}{2})^2} = \boxed{\sqrt{\frac{13}{2}}} $
Answers
For Printing
Revision Questions
The questions included are optional, but here if you want some extra practice.
- Engineering Mathematics 7th edition, Stroud and Dexter : Pages 519-543
- Advanced Engineering Mathematics 5th edition, Stroud and Dexter : Pages 771-784, 812-817
- Vector Questions Part A Vector Questions Part B : Lots of questions that develop in difficulty.
- A-Level Various Exam Questions : More practice getting technique and understanding. Particularly try ‘planes’ and ‘geometric problems’.
- A-Level OCR Exam Questions : Past A-Level exam questions. You will need to look to the past OCR markschemes for the answers.
- A-Level Various Exam Questions : Scroll and find past A-Level exam questions by various exam boards.