Sequence, Series, Limits and Convergence Tutorial Sheet, Sheet #5B
Learning targets
- Suggest formulae for the $n$th term of given sequences
- Use the binomial distribution
- Calculate the sum of a series
- Use the standard summation formulae
- Identify the limiting values of sequence
- Determine when/whether a series is (absolutely) convergent
Additional Resources
Tutorials
- Sequences and Series : Extra video by Sam recapping sequences and series from the lecture.
Problem sheet
Skill Building Questions
Problem 1.
Suggest a formula for the $n$th term of the following sequences:
(a) $3, -5, 7, -9, 11,…$
Because the numbers alternate from positive to negative we need to include $(-1)^{n+1}$.
$\Rightarrow\boxed{a_n=(-1)^{n+1}.(2n+1)}$
(b) $2,\frac{3}{2},\frac{4}{3},\frac{5}{4},\frac{6}{5},…$
$a_n=\frac{2 + (n-1)}{1+(n-1)}$
$\Rightarrow\boxed{a_n=\frac{n+1}{n}}$
(c) $\frac{2}{3},\frac{3}{2\times{}4},\frac{4}{3\times{}5},\frac{5}{4\times{}6},\frac{6}{5\times{}7},…$
(d) $1, 0,-e^2,0,e^4,…$
Problem 2.
Find the third, sixth and ninth term of the sequence given by the formula:
(a) $ \sum_{n=1}^{\infty}\ \left(\frac{n^2-n-6}{n+2}\right) $
(b) $ \sum_{n=1}^{\infty}\ \left(\text{sin}[ \left(n+1\right)\frac{\pi{}}{3}]\right) $
(c) $ \sum_{n=3}^{\infty}\ \left(\binom{n}{2}-\binom{n}{3} \right)$
Tip: Use the binomial coefficient $\binom{n}{k}=\frac{n!}{k!(n-k)!}$
Problem 3.
Evaluate the following:
(a) $\sum_{n=1}^{20}\left(0.2n+5\right)$
$\Rightarrow S_n= \frac{n}{2}(2a + d(n - 1)) \\ = \frac{20}{2}(2(0.2+5) + (0.2)(20 - 1)) \\ = 10*14.2 \\ = \boxed{142}$
(b) $\sum_{n=1}^8n\left(3+2n+n^2\right)$
$\Rightarrow 3\sum_{n=1}^8n \ + \ 2\sum_{n=1}^8n^2 \ +\ \sum_{n=1}^8n^3\ \\ = 3(\frac{8(8+1)}{2}) + 2(\frac{8(8+1)(16+1)}{6}) + \frac{64(8+1)^2}{4} \\ = 108 + 408 + 1296 \\= \boxed{1812}$
(c) $\sum_{r=1}^nr\left(r+3\right)$
$\Rightarrow \sum_{r=1}^nr^2 \ + 3\sum_{r=1}^nr \\ \\ = \frac{n(n+1)(2n+1)}{6} + 3(\frac{n(n+1)}{2}) \\ \\ = \frac{n}{6}((n+1)(2n+1) +9(n+1)) \\ \\ = \frac{n}{6}(2n^2+12n+10) \\ \\ = \frac{n}{3}(n^2+6n+5) \\ \\ =\boxed{\frac{n}{3}\left(n+1\right)\left(n+5\right)}$
(d) $\sum_{r=1}^n{\left(r+1\right)}^3$
$\Rightarrow \sum_{r=1}^nr^3 \ + 3\sum_{r=1}^nr^2 \ +3\sum_{r=1}^nr \ +\sum_{r=1}^n1 \\ \\ = \frac{n^2(n+1)^2}{4} + \frac{n(n+1)(2n+1)}{2} + 3(\frac{n(n+1)}{2}) + n \\ \\ = \frac{n}{4}(n(n+1)^2 + 2(n+1)(2n+1) + 6(n+1) + 4) \\ \\ = \frac{n}{4}(n^3 + 2n^2 + n + 4n^2 + 6n + 2 + 6n + 6 + 4) \\ \\ = \boxed{\frac{n}{4}(n^3 + 6n^2 + 13n + 12)}$
Problem 4.
Find the sum of $n$ terms of the following:
(a) $S_n=1^2+3^2+5^2+ . . . +{\left(2n-1\right)}^2$
(b) $S_n=5-\frac{5}{2}+\frac{5}{4}-\frac{5}{8}+ . . . +\frac{ {\left(-1\right) }^{n-1}5}{2^{n-1}}$
$= 5\frac{1-(\frac{-1}{2})^n}{1-(\frac{-1}{2})} \\ = 5\frac{1+\frac{\left(-1\right)^{n+1}}{2^n}}{\frac{3}{2}} \\ \Rightarrow\boxed{S_n=\frac{10}{3}\left\{1+\frac{\left(-1\right)^{n+1}}{2^n}\right\}\ }$
Problem 5.
Find the limiting values of the following:
(a) $\frac{ {3x}^2+5x-4}{ {5x}^2-x+7}\ \text{as} \ x\rightarrow{}\infty{}$
$\boxed{\frac{ {3x}^2+5x-4}{ {5x}^2-x+7}\rightarrow{}\frac{3}{5}, \text{ as } x\rightarrow{}\infty{}}$
(b) $\frac{x^2+5x-4}{ {2x}^2-3x+1}\ \text{as}\ x\rightarrow{}\infty{}$
$\boxed{\frac{x^2+5x-4}{ {2x}^2-3x+1}\rightarrow{}\frac{1}{2}, \text{ as } x\rightarrow{}\infty{}}$
Problem 6.
(a) Using the standard summation formulae, find an expression for $S=\sum_{r=1}^{n}\ (2-4r)^2$ in terms of $n$. Give your answer in a fully factorised form.
(b) Hence evaluate $S=\sum_{r=20}^{60}\ (2-4r)^2$
Problem 7.
(a) Show that $S=\sum_{r=1}^{n}\ (4r-2) = 2n^2$
(b) Show that $\frac{ \sum_{r=1}^{n}\ (2r-1)}{\sum_{r=n+1}^{2n}\ (2r-1)} = k$, where $k$ is constant to be determined.
(c) Use standard series formulae to show that $\sum_{r=1}^{n}\ r^2(6-8r) = n(n+1)(1-2n^2)$
Problem 8.
Determine whether each of the following series converges or diverges:
(a) $\sum_{n=1}^{\infty{}}\frac{n}{n^2+1}$
Solution:
Using $n^{th}$ term test (or "Test for Divergence" as written in the notes), it is indicated that as $n$ goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Note: Here it is not possible to apply the ratio test as $\lim_{n\rightarrow\infty}{\frac{a_{n+1}}{a_n}}=1$. $$ \lim_{n\rightarrow\infty}{\frac{(n+1)(n^2+1)}{((n+1)^2+1)(n)}}=\lim_{n\rightarrow\infty}{\frac{n^3+n^2+n+1}{n^3+2n^2+2n}}=1 $$ Instead, we can use the "Limit Comparison Test". We choose an arbitrary $b_n$ in which for all $n=1,2,3, ...,\infty$, $b_n>0$. Then if $\lim_{n\rightarrow\infty}{\frac{a_n}{b_n}=c>0}$: $$ \text{either } b_n \text{ converges, so then } a_n \text{ converges} $$ $$ \text{or } b_n \text{ diverges, so then } a_n \text{ diverges} $$ Here, let $b_n=\frac{1}{n}$. Note that we can also pick other functions for $\ b_n $ but choosing $\frac{1}{n}$ or $\frac{1}{n^2}$ is a common and a safe option for this test.
$$ \lim_{n\rightarrow\infty}{\frac{\frac{n}{n^2+1}}{\frac{1}{n}}}=\frac{n^2}{n^2+1}=1>0. $$ Hence, since $\sum_{n=1}^{\infty}{b_n}$ diverges, $\sum_{n=1}^{\infty}{a_n}$ also diverges.
Note: if it's unclear to you why $\sum_{n=1}^{\infty}{b_n}$ is divergent this can be verified using the p-series test which says: if $a_n = n^{-p}$, and $p > 1$ then the series converges.
$b_n = \frac{1}{n} = n^{-1}$
In this case $p$ isn't greater than 1 so the series does not converge: it diverges.
(b) $\sum_{n=0}^{\infty{}}\frac{1}{\left(2n+1\right)!}$
Solution:
Using $n^{th}$ term test (or "Test for Divergence" as written in the notes), it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). We can use the ratio test: $$ \lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}} =\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{1}{\left(2\left(n+1\right)+1\right)!}\times{}\frac{\left(2n+1\right)!}{1}\right\vert{}=\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{\left(2n+1\right)!}{\left(2n+3\right)!}\right\vert{}=0}} $$ $\therefore$ The series is convergent.
Note: when testing for convergence the ratio test is the most common test to try first after the $n^{th}$ term test (or "Test for Divergence" as written in the notes). If that test fails then try another one.
(c) $\frac{x}{1\times{}2}+\frac{x^2}{2\times{}3}+\frac{x^3}{3\times{}4}+…,\ \text{for}\ -1 < x < +1$
Solution:
The equation for sum of the series is: $$ \sum_{n=1}^{\infty{}}\frac{x^n}{n(n+1)} $$ Using $n^{th}$ term test (or "Test for Divergence" as written in the notes), it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Using the ratio test: $$ \lim_{x\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}=}\lim_{x\rightarrow{}\infty{}}{\left\vert{}\frac{ {(x}^{n+1}). [ n(n+1) ] }{\left[ \left(n+1\right)(n+2) \right] .x^n}\right\vert{}}=\left\vert{}x\right\vert{} $$ Therefore, the series converges for $\left\vert{}x\right\vert{}<1$.
i.e. since the limit isn't equal to 1, then as long as $\left\vert{}x\right\vert{}$ is less than one the series converges.
(d) $\sum_{n=1}^{\infty{}}\frac{ {1+3n}^2}{ {1+n}^2}$
Solution:
Using $n^{th}$ term test (or "Test for Divergence" as written in the notes), it is indicated that as $n$ index goes to infinity, the terms go to non-zero value (i.e. the series is divergent at this stage). We can use the ratio test to verify that it diverges as well: $$ \lim_{n\rightarrow{}\infty{}}{\frac{1+3n^2}{1+n^2}=3} $$
Problem 9.
Find the range of values of $X$ for which the following series are absolutely convergent:
(a) $\frac{X}{27}+\frac{X^2}{125}+…+\frac{X^n}{ {\left(2n+1\right)}^3}+…$
Solution: Using $n^{th}$ term test, it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Using the ratio test: $$ \lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}} $$ $$ =\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{X^{(n+1)}}{ {(2\left(n+1\right)+1)}^3}\times{}\frac{ {(2n+1)}^3}{X^n}\right\vert{}} $$ $$ =\left\vert{}X\right\vert{}\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{ {(2n+1)}^3}{ {(2n+3)}^3}\right\vert{}=\vert{}X\vert{}} $$ Convergent for $-1 < X < 1$. Now check if the endpoints are converging: $$ At\ X=1,\lim_{x\rightarrow{}1}{\sum_{n=1}^{\infty{}}\frac{X^n}{ {(2n+1)}^3}\Rightarrow{}\text{convergent}} $$ $$ At\ X=-1,\\ \lim_{x\rightarrow{}-1}{\sum_{n=1}^{\infty{}}\frac{X^n}{ {(2n+1)}^3}\Rightarrow{}\text{convergent}} $$
(b) $ \sum_{n=1}^{\infty{}}\frac{(n+1)}{n^3}X^n $
Solution: Using $n^{th}$ term test, it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Using the ratio test: $$ \lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}}=\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{\left(n+2\right)X^{(n+1)}}{ {(n+1)}^3}\times{}\frac{n^3}{\left(n+1\right)X^n}\right\vert{}} $$ $$ =\left\vert{}X\right\vert{}\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{n^4+2n^3}{n^4+{4n}^3+{6n}^2+4n+1}\right\vert{}=\vert{}X\vert{}} $$ Convergent for $-1< X < 1$. Now check if the endpoints are converging: $$ At\ X=1,\\ \lim_{x\rightarrow{}1}{\sum_{n=1}^{\infty{}}\frac{\left(n+1\right)*X^n}{n^3}} \Rightarrow{}\text{convergent} $$ $$ At\ X=-1,\\ \lim_{x\rightarrow{}-1}{\sum_{n=1}^{\infty{}}\frac{\left(n+1\right)*X^n}{n^3}} \Rightarrow{} \text{convergent} $$
(c) $ \sum_{n=1}^{\infty{}}(\ln{n)}X^n $
Solution: Using $n^{th}$ term test, it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Using the ratio test: $$ \lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}=}\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{ {\ln{\left(n+1\right)}.X}^{n+1}}{\ln{\left(n\right)}{.X}^n}\right\vert{}}=\left\vert{}X\right\vert{} $$ Therefore, converges for $\left\vert{}X\right\vert{}<1$. Now check if the endpoints are converging: $$ At\ X=1,\\ \lim_{x\rightarrow{}1}{\sum_{n=1}^{\infty{}}\ln{\left(n\right)}}\Rightarrow{} \text{divergent} $$ $$ At\ X=-1,\\ \lim_{x\rightarrow{}-1}{\sum_{n=1}^{\infty{}}} {(-1)}^n\ln{\left(n\right)}\Rightarrow{} \text{divergent} $$ Note: The $n^{th}$ term test showed that $\lim_{n\to\infty}$ of $a_n$ goes to zero only for $-1 < X <1$. However, the test only shows whether the function diverges and does not test the convergency. Hence, the ratio test must be conducted.
(d) $ \sum_{n=0}^{\infty{}}\frac{3^nX^n}{n!} $
Solution: Using $n^{th}$ term test, it is indicated that as $n$ index goes to infinity, the terms go to zero (i.e. the series is not divergent at this stage). Using the ratio test: $$ \lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{a_{n+1}}{a_n}\right\vert{}=}\lim_{n\rightarrow{}\infty{}}{\left\vert{}\frac{3^{n+1}X^{n+1}}{\left(n+1\right)!}\times{}\frac{n!}{3^nX^n}\right\vert{}}= \frac{3\left\vert{}X\right\vert{}}{n+1}=0 $$ The function will always converge no matter what the value of $X$ is.
Exam Style Questions
Problem 10.
An investment fund offers three investment strategy packages to its clients if they invest exactly £500,000. The first option is an annual return of 16%, but this is not compounded each year (i.e. the profit from each year is not reinvested). The second option offers a compounded daily return of 0.03%. The third option simply pays you an increasing dividend of £1 on the first day, followed by £2 on the second, £3 on the third and so on.
(a) Calculate the profit after 4 years for each of the three options.
The annual return will be: $ \frac{16}{100} \times £500,000 = £80,000 $ So the profit after four years will be: $ 4 \times £80,000 \Rightarrow \boxed{£320,000} $
Option 2:
To calculate compound interest we use: $P[(1+i)^{n} - 1] \\ P = \text{initial balance, } i = \text{interest rate, and } n = \text{number of compounding periods.}$
$ £500,000 \times (1.0003^{4 \times 365} − 1) \Rightarrow \boxed{£274,751.56} \\ $ Option 3:
Method 1: We can calculate the total profit by creating a formula for the sum of the profit each day for 4 years. $\sum_{n=0}^{4 \times 365}{n} \Rightarrow \boxed{£1,066,530} \\ $
Method 2: We can calculate the sum of the profit using the formula for the sum of an arithmetic series. $\text{The sum of this series is: } \quad S_n = \frac{n}{2}(2a + (n - 1)d) = \frac{n(n+1)}{2} \\ \therefore (4 \times 365)\frac{(4 \times 365 + 1)}{2} \Rightarrow \boxed{£1,066,530}$
(b) Which option offers the best return after 40 years?
Option 1:
The return will be: $ £3,200,000 $
Option 2:
The return will be: $ £39,392,804 $
Option 3:
The return will be: $ £106,587,300 $
So the option with the best return is $\Rightarrow \boxed{\text{Option 3}}$
(c) Draw a graph showing the profit vs. time for the three options over 40 years.
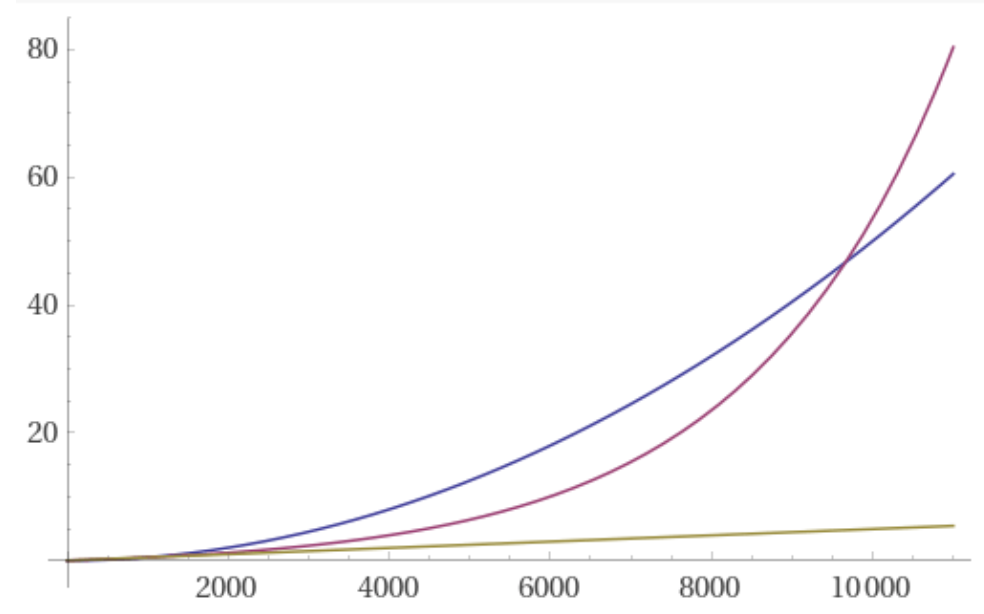 Yellow = option 1
Yellow = option 1
Pink = option 2
Purple = option 3
(d) Write down an expression for the difference between the profits of the second and third options as a function of the number of days since investing, 𝑁.
(e) Give an interpretation of the roots of this function.
Extension Questions
Problem 11.
Let $ \ S_n \ $ be a sequence given by $ \ S_n = \frac{1}{n+1} + \frac{1}{n+2} + … + \frac{1}{2n}$.$\ $ Show that the sequence is increasing.
Problem 12.
Fid the missing number in the following sequence: $\ \ 61, \ 52, \ 63, \ 94, \ ?, \ 18,… $
i.e. read the number from right to left. The sequence then becomes:
$16, \ 25, \ 36, \ 49, \ ?, \ 81,... $
Now you just have a sequence of the squared numbers starting at 4:
$4^2, \ 5^2, \ 6^2, \ 7^2, \ ?, \ 9^2,... $
so the missing number will be $8^2 = 64$ and if we reverse the digits we have our final answer $\Rightarrow\boxed{46}$
Answers
For Printing
Revision Questions
The questions included are optional, but here if you want some extra practice.
- Engineering Mathematics 7th edition, Stroud and Dexter : Pages 605-610, 626-662
- Series Questions : Nice algebra with some ‘finding the constants’, the enrichment questions are fun to try!
- More Series Questions : Involves convergence and divergence, nice questions using algebra, proofs, sums, good for understanding.
- 3D Curve Sketching : Evaluation of limits, convergence - you may be able to use Wolfram to solve questions that are tagged with other methods. You can ignore integration ones, though Sam could throw anything…