Complex Numbers Tutorial Sheet, Sheet #6
Learning targets
- Convert complex numbers from their Cartesian form to their Polar or exponential form
- Divide, multiply, add and subtract Complex numbers
- Manipulate complex numbers to find real and imaginary parts; find the absolute value and conjugate
- Plot complex numbers and an Argand diagram
- Understand and use de Moivres theorem
Additional Resources
Tutorials
- Imaginary Numbers are Real : Interesting video to add more understanding.
- Interactive Graph : Tutorial and interactive site that takes you through and allows you to visualise multiplying and dividing complex numbers.
Problem sheet
Skill Building Questions
Problem 1.
Express the flowing complex numbers in their polar form, $r(\cos\theta+\mathrm{i}\sin\theta)$ and exponential form, $re^{i\theta }$.
(a) $z=3+4\mathrm{i}$
$r=\| z \|=\sqrt{3^2+4^2}=\sqrt{25}=5$
Find the argument $arg(z)$ (angle $\theta$):
$\theta= \text{arg}(z) =\tan^{-1}(\frac{\text{imaginary part}}{\text{real part}})= \tan^{-1}(\frac{4}{3}) = 53.13^\circ$
Polar Form
$z=a+b\mathrm{i}=r(\cos\theta+\mathrm{i}\sin\theta)$
$\Rightarrow \boxed{\text{Therefore } z=5(\cos 53.13^\circ+\mathrm{i}\sin 53.13^\circ)}$
Exponential Form
$z = re^{i\theta }$
$\Rightarrow \boxed{\text{Therefore } 5e^{53.13^\circ i}}$
(b) $z=-3-\mathrm{i}$
Plot $z$ on an Argand diagram:
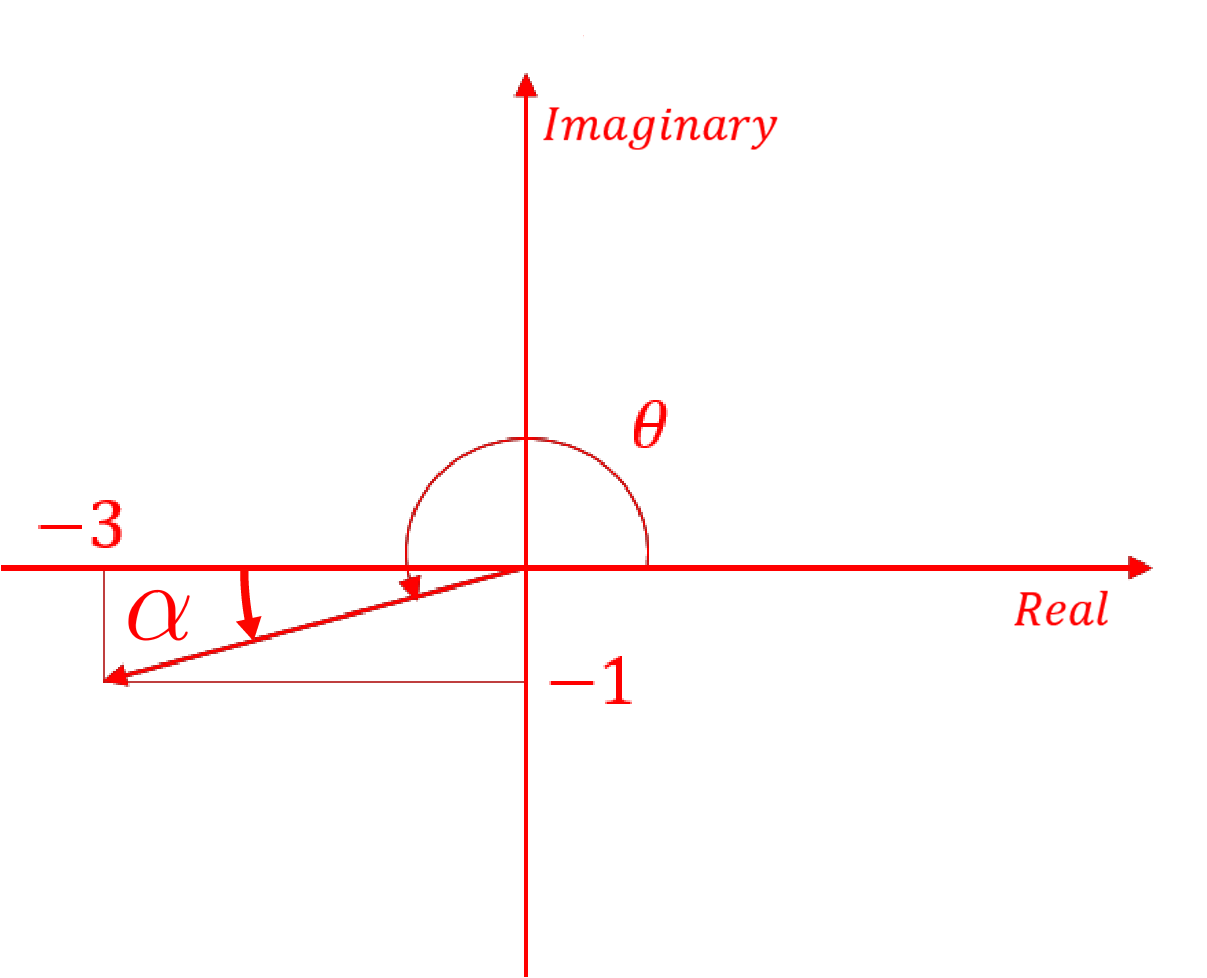
$\alpha=\tan^{-1}(\frac{-1}{-3})=\tan^{-1}(\frac{1}{3})=18.43^\circ$ As a result, $arg(z) = \theta = 18.43^\circ + 180^\circ = 198.43^\circ$
Polar Form
$z=a+b\mathrm{i}=r(\cos\theta+\mathrm{i}\sin\theta)$
$\Rightarrow \boxed{\text{Therefore } z= 3.16(\cos198.43^\circ+\mathrm{i}\sin198.43^\circ)}$ Alternative answer: $z= 3.16(\cos(-161.57^\circ)+\mathrm{i}\sin(-161.57^\circ))$
Exponential Form
$z = re^{i\theta }$
$\Rightarrow \boxed{\text{Therefore } 3.16e^{198.43^\circ i}}$
(c) $z=-\mathrm{i}$
Find the argument $arg(z)$ (angle $\theta$): $\theta=\mathrm{arg}(z)=\tan^{-1}(\frac{-1}{0})+180^\circ=\tan^{-1}(\infty)+180^\circ=90^\circ+180^\circ=270^\circ $
Polar Form
$z=a+b\mathrm{i}=r(\cos\theta+\mathrm{i}\sin\theta)$
$\Rightarrow \boxed{\text{Therefore }z=1(\cos270^\circ+\mathrm{i}\sin270^\circ)}$ Alternative answer: $z=1(\cos-90^\circ+\mathrm{i}\sin-90^\circ)$
Exponential Form
$z = re^{i\theta }$
$\Rightarrow \boxed{\text{Therefore } e^{270^\circ i}}$
(d) $z=3-4\mathrm{i}$
Plot $z$ on an Argand diagram:
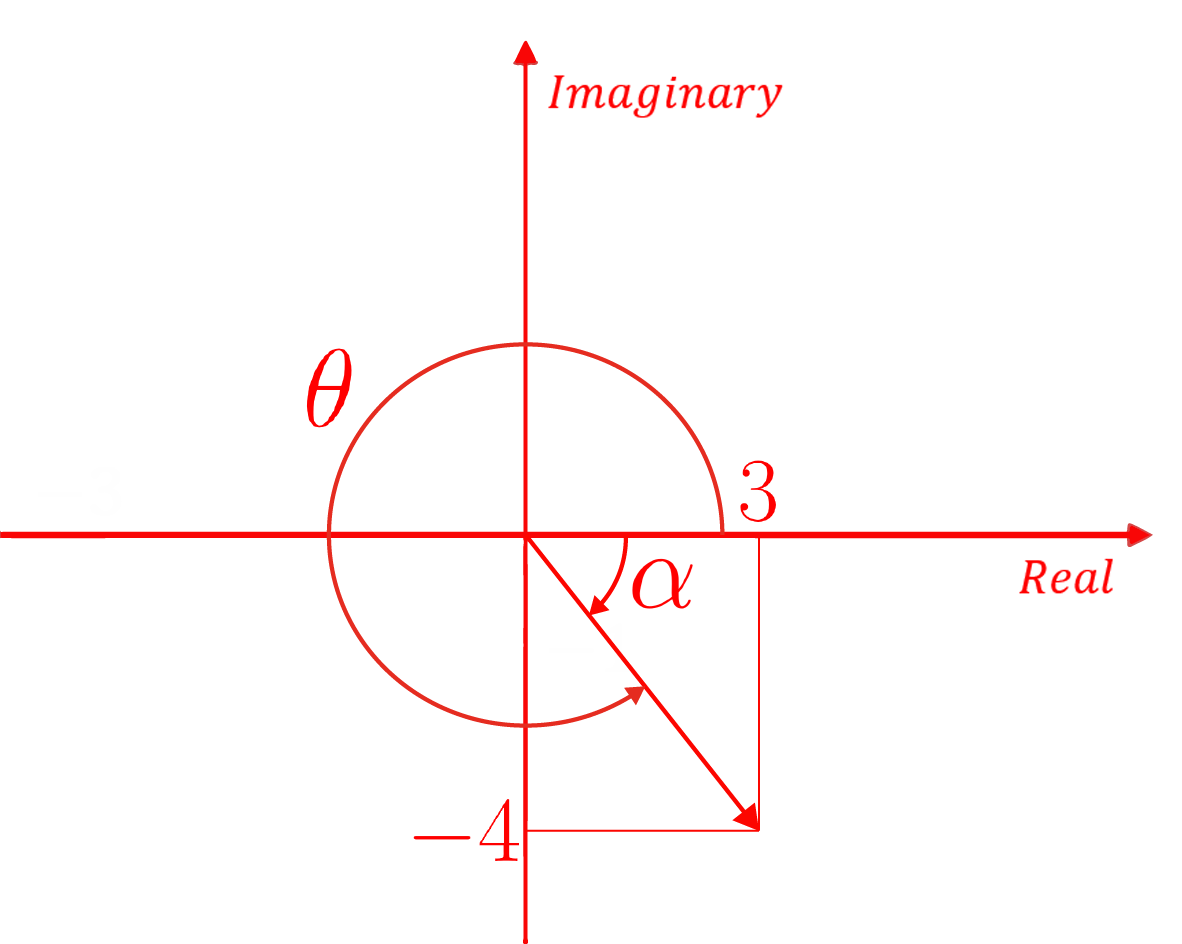
$\alpha = \tan^{-1}(\frac{4}{3})=53.13$
$\theta=\mathrm{arg}(z)=360^\circ-53.13^\circ=306.87^\circ$
Polar Form
$z=a+b\mathrm{i}=r(\cos\theta+\mathrm{i}\sin\theta)$
$\Rightarrow \boxed{\text{Therefore } z= 5(\cos306.87^\circ+\mathrm{i}\sin306.87^\circ)}$ Alternative answer: $z=5(\cos-53.13^\circ+\mathrm{i}\sin-53.13^\circ)$
Exponential Form
$z = re^{i\theta }$
$\Rightarrow \boxed{\text{Therefore } 5e^{306.87^\circ i}}$
Complex Number Plotter Visualization
To help with intuition when answering these questions, here is a visualization built in Manim. You can play around with it here!
Problem 2.
Consider the complex numbers $z_1=2+4\mathrm{i}$ and $z_2=4-7\mathrm{i}$.
(a) Find $z_1+z_2$
$ z_1+z_2=(2+4\mathrm{i})+(4-7\mathrm{i})=(2+4)+(4-7)\mathrm{i}=\boxed{6-3\mathrm{i}}$
(b) Find $z_1-z_2$
(c) Find $z_1z_2$
$z_1z_2=(2+4\mathrm{i})(4-7\mathrm{i})=2\times4-2\times7\mathrm{i}+4\times4\mathrm{i}-4\times7\mathrm{i^2}$
Collect real and complex terms: $8-14\mathrm{i}+16\mathrm{i}+28= \boxed{36+2\mathrm{i}}$
(d) Find $\frac{z_1}{z_2}$
Note:
Simplify a complex fraction $\frac{a+b\mathrm{i}}{c+d\mathrm{i}}$ by rationalizing the denominator - multiplying the fraction with the complex conjugate of the denominator over itself (effectively multiplying by $1$), i.e., $\frac{a+b\mathrm{i}}{c+d\mathrm{i}}\cdot\frac{c-d\mathrm{i}}{c-d\mathrm{i}}$
Complex Number Multiplication Visualization
To help with intuition when answering these questions, here is a visualization built in Manim. You can play around with it here!
Problem 3.
(a) Find the real and imaginary part of $z = \frac{\mathrm{i}-4}{2\mathrm{i}-3}$
$z=\frac{\mathrm{i}-4}{2\mathrm{i}-3}=\frac{\mathrm{i}-4}{2\mathrm{i}-3}\cdot\frac{2\mathrm{i}+3}{2\mathrm{i}+3}=\frac{-12-2+3\mathrm{i}-8\mathrm{i}}{-4-9}=\frac{14}{13}+\frac{5}{13}\mathrm{i}$.
Therefore, $\boxed{\mathrm{Re}(z)=\frac{14}{13}}$ and $\boxed{\mathrm{Im}(z)=\frac{5}{13}}$
(b) Find the absolute value and the conjugate of $z = (1+\mathrm{i})^6$
Using De Moivre's Theorem: $(\sqrt{2}(\cos\frac{\pi}{4}+\mathrm{i}\sin\frac{\pi}{4}))^6=8(\cos\frac{3\pi}{2}+\mathrm{i}\sin\frac{3\pi}{2})=-8i$
Hence, $\boxed{|z|=8 \text{ and } \overline{z}=8\mathrm{i}}$
(c) Find the absolute value and the conjugate of $w = \mathrm{i}^{17}$
(d) Simplify the complex number $\frac{1+\mathrm{i}}{1-\mathrm{i}}-(1+2\mathrm{i})(2+2\mathrm{i})+\frac{3-\mathrm{i}}{1+\mathrm{i}}$
$\frac{1+\mathrm{i}}{1-\mathrm{i}}=\frac{1+\mathrm{i}}{1-\mathrm{i}}\cdot\frac{1+\mathrm{i}}{1+\mathrm{i}} = \frac{1-i^{2}+2\mathrm{i}}{2}=\mathrm{i}$ $-(1+2\mathrm{i})(2+2\mathrm{i})=2-6\mathrm{i}$ $\frac{3-\mathrm{i}}{1+\mathrm{i}}=\frac{3-\mathrm{i}}{1+\mathrm{i}}\cdot\frac{1-\mathrm{i}}{1-\mathrm{i}}=\frac{3+\mathrm{i}^2-3\mathrm{i}-\mathrm{i}}{1-\mathrm{i}^2}=1-2\mathrm{i}$
Therefore:
$\frac{1+\mathrm{i}}{1-\mathrm{i}}-(1+2\mathrm{i})(2+2\mathrm{i})+\frac{3-\mathrm{i}}{1+\mathrm{i}}=\mathrm{i}+2-6\mathrm{i}+1-2\mathrm{i}=\boxed{3-7\mathrm{i}}$
(e) Simplify the complex number $2\mathrm{i}(\mathrm{i}-1)+(\sqrt{3}-\mathrm{i})^3+(1+\mathrm{i})(1-\mathrm{i})$
Problem 4.
Plot the flowing complex numbers on an Argand diagram:
(a) $z=3+2\mathrm{i}$
(b) $z=4-5\mathrm{i}$
(c) $z=-2-\mathrm{i}$
(d) $| z |=3$
$|z|=|x+\mathrm{i}y|=3$ $\sqrt{x^2+y^2}=3$ $\Rightarrow$ Therefore: $x^2+y^2=9$ The solution ($x^2+y^2=9$) consists of all the points lying on the circle of radius 3 with center (0,0).
Problem 5.
Write the following complex number in polar and exponential forms
$z=\frac{1}{2}-\frac{\sqrt{3}}{2}\mathrm{i}$
Plot $z$ on an Argand diagram
$\theta=\tan^{-1}(\sqrt{3})=\frac{\pi}{3}$ Therefore $\mathrm{arg}(z)=-\frac{\pi}{3}$ or alternatively: $\mathrm{arg}(z)=\frac{5\pi}{3}$
Complex number $z$ in polar form:
$z=\cos\frac{-\pi}{3}+\mathrm{i}\sin\frac{-\pi}{3}=\boxed{\cos\frac{\pi}{3}-\mathrm{i}\sin\frac{\pi}{3}}$ or: $\cos\frac{5\pi}{3}+\mathrm{i}\sin\frac{5\pi}{3}$ In exponential form: $\boxed{e^{-\frac{\pi}{3}\mathrm{i}}}$ or: $e^{\frac{5\pi}{3}\mathrm{i}}$
Problem 6.
Application of de Moivre’s theorem.
(a) Find $(\cos\theta+\mathrm{i}\sin\theta)^{-10}$ in the form $(\cos(A\theta)-\mathrm{i}\sin(B\theta))$
(b) Simplify the flowing expression: $\frac{\cos2\theta+\mathrm{i}\sin2\theta}{\cos3\theta+\mathrm{i}\sin3\theta}$
$=\frac{(\cos\theta+\mathrm{i}\sin\theta)^2}{(\cos\theta+\mathrm{i}\sin\theta)^3}$ . $\frac{(\cos\theta+\mathrm{i}\sin\theta)^2}{(\cos\theta+\mathrm{i}\sin\theta)^3}$
$=\frac{(\cos\theta+\mathrm{i}\sin\theta)^2}{(\cos\theta+\mathrm{i}\sin\theta)^2(\cos\theta+\mathrm{i}\sin\theta)}$
$=\frac{1}{\cos\theta+\mathrm{i}\sin\theta}(\frac{\cos\theta-\mathrm{i}\sin\theta}{\cos\theta-\mathrm{i}\sin\theta})$
$=\boxed{\cos\theta-\mathrm{i}\sin\theta}$
(c) Prove that $\cos3\theta = \cos^3\theta-3\cos\theta\sin^2\theta$
By de Moivre’s theorem: $\cos3\theta+\mathrm{i}\sin3\theta =(\cos\theta+\mathrm{i}\sin\theta)^3 $
$=\cos^3\theta+3\cos^2\theta(\mathrm{i}\sin\theta)+3\cos\theta(\mathrm{i}\sin\theta)^2+(\mathrm{i}\sin\theta)^3$ . $\cos^3\theta+3\mathrm{i}\cos^2\theta\sin\theta-3\cos\theta\sin^2\theta-\mathrm{i}\sin^3\theta $
$=\cos^3\theta-3\cos\theta\sin^2\theta+\mathrm{i}(3\cos^2\theta\sin\theta-\sin^3\theta) $
Comparing real parts of each side of the equation above, you obtain: $$\boxed{\cos3\theta = \cos^3\theta-3\cos\theta\sin^2\theta}$$
Exam Style Questions
Problem 7.
(a) Write down the modulus and argument of the complex number $4-4\mathrm{i}$.
Plotting $z^5$ on an Argand diagram:
From the Argand diagram above: $\mathrm{arg}(4-4\mathrm{i})=arctan(\frac{-4}{4})$
$\Rightarrow\boxed{-\frac{\pi}{4}}$ alternatively, $\boxed{\frac{7\pi}{4}}$
(b) Solve the equation $z^5 = 4-4\mathrm{i}$, expressing your answers in the exponential form.
Rewrite the argument for the complex number, $4-4\mathrm{i}$, in its exponential form: $4\sqrt{2}e^{i\frac{7\pi}{4}}$
According to De Moivre's theorem:
$z^n$ = $(re^{i\theta})^n$ = $r^n e^{in\theta}$
As the value is $z^5$, n = 5.
$\sqrt[5]{4\sqrt{2}}$ = $\sqrt{2}$
$\frac{7\pi}{4}$ / 5 = $\frac{7\pi}{20}$
There will be 5 solutions before the angle 'repeats'.
Adding/subtracting $\frac{2\pi}{5}$ from $\frac{7\pi}{20}$ = ${\frac{-17\pi}{20}, \frac{-9\pi}{20}, \frac{-\pi}{20}, \frac{7\pi}{20}, \frac{15\pi}{20}}$
Putting it together, solutions in the exponential are: $\boxed{z_1=\sqrt{2}e^{\frac{-17\pi}{20}i}}$, $\boxed{z_2=\sqrt{2}e^{\frac{-9\pi}{20}i}}$, $\boxed{z_3=\sqrt{2}e^{\frac{-\pi}{20}i}}$, $\boxed{z_4=\sqrt{2}e^{\frac{7\pi}{20}i}}$, and $\boxed{z_5=\sqrt{2}e^{\frac{3\pi}{4}i}}$
Method 2
Rewrite the argument for the complex number, $4-4\mathrm{i}$, in its general form: $2n\pi-\frac{\pi}{4}$, where n is an integer. Note: For any integer n, $\cos(2n\pi-\frac{\pi}{4})=\cos(-\frac{\pi}{4})$. Likewise for $\sin(-\frac{\pi}{4})$.
Now, $z^5=\cos(2\pi-\frac{\pi}{4})+\mathrm{i}\sin(2\pi-\frac{\pi}{4})$
Model the solutions, $z_n$, to $z^5=4-4\mathrm{i}$ as complex numbers in polar form, i.e.: $z_n=r(\cos\theta+\mathrm{i}\sin\theta)$
If $z_n=r(\cos\theta+\mathrm{i}\sin\theta)$, then by de Moivres theorem: $z^{5}=r^{5}(\cos5\theta+\mathrm{i}\sin5\theta)$ $=4\sqrt{2}(\cos\frac{\pi}{4}-\mathrm{i}\sin\frac{\pi}{4})$
Compare magnitudes: $r^5=4\sqrt{2}, r=\sqrt{2}$
Compare arguments: $5\theta=2n\pi-\frac{\pi}{4}, \theta=(8n-1)\frac{\pi}{20}$
For appropriate values of n, so that $\theta$ lies between $-\pi$ and $\pi$: $$n=-2\quad\Rightarrow\quad\theta=\frac{-17\pi}{20}$$ $$n=-1\quad\Rightarrow\quad\theta=\frac{-9\pi}{20}$$ $$n=0\quad\Rightarrow\quad\theta=\frac{-\pi}{20}$$ $$n=1\quad\Rightarrow\quad\theta=\frac{7\pi}{20}$$ $$n=2\quad\Rightarrow\quad\theta=\frac{15\pi}{20} \text{ or } \frac{3\pi}{4}$$ Therefore solutions in exponential are: $\boxed{z_1=\sqrt{2}e^{\frac{-17\pi}{20}i}}$, $\boxed{z_2=\sqrt{2}e^{\frac{-9\pi}{20}i}}$, $\boxed{z_3=\sqrt{2}e^{\frac{-\pi}{20}i}}$, $\boxed{z_4=\sqrt{2}e^{\frac{7\pi}{20}i}}$, and $\boxed{z_5=\sqrt{2}e^{\frac{3\pi}{4}i}}$
(c) State the solution, to part (b), with the smallest positive argument and find the real part of it (in polar form).
$\boxed{Re({\sqrt{2}e^{\frac{7\pi}{20}i})} =\sqrt{2}\cos\left(\frac{7\pi}{20}\right)}$
Problem 8.
Find the value of $x$ and $y$ in the equation $(x+iy)(3+4i) = 3-4i$ given that $x \in \mathbb{R}$ and $y\in \mathbb{R}$.
=$\frac{(3-4i)(3-4i)}{(3+4i)(3-4i)}$
=$\frac{9-12i-12i-16i^2}{9-12i-12i+16i^2}$
=$\frac{-7-24i}{25}$
Therefore $\boxed{x = \frac{-7}{25}}$ and $\boxed{y = \frac{-24}{25}}$
Problem 9.
It is given that $z = \frac{1+8i}{1-2i}$. Show that $arctan(8) + arctan(2) + arctan(\frac{2}{3}) = \pi$.
=$\frac{(1+8i)(1+2i)}{(1-2i)(1+2i)}$
=$\frac{1+2i+8i-16}{1+4}$
=$\frac{-15+10i}{5}$
=$-3+2i$
$arg(\frac{1+8i}{1-2i})$ = $arg(-3+2i)$
$arg(1+8i)-arg(1-2i)$ = $arg(-3+2i)$
$arctan(\frac{8}{1}) - arctan(\frac{-2}{1}) = \pi - arctan(\frac{2}{3})$
$arctan(8) + arctan(2) = \pi - arctan(\frac{2}{3})$
$arctan(8) + arctan(2) + arctan(\frac{2}{3}) = \pi $
Extension Questions
Problem 10.
Find a solution of the equation $cos(z) = 2isin(z), z \in\mathbb{C} $
$\Rightarrow\quad cosh(iz) = 2sinh(iz)$
$\Rightarrow\quad \frac{1}{2}(e^{iz}+e^{-iz}) = 2.\frac{1}{2}(e^{iz}-e^{-iz})$
$\Rightarrow\quad e^{iz}+e^{-iz} = 2e^{iz}-2e^{-iz}$
$\Rightarrow\quad e^{iz} = 3e^{-iz}$
$\Rightarrow\quad e^{2iz} = 3$
$\Rightarrow\quad 2iz = \ln{3} + iArg3$
$\Rightarrow\quad 2iz = \ln{3} + i(0+2k\pi)$
$\Rightarrow\quad 2iz = \ln{3} + 2ki\pi$
$\Rightarrow\quad z = \frac{1}{2i}\ln{3} + k\pi$
$\therefore\quad z = \frac{1}{2i}\ln{3}, k \in\mathbb{Z}$
Answers
For Printing
Revision Questions
The questions included are optional, but here if you want some extra practice.
- Engineering Mathematics 7th edition, Stroud and Dexter : Pages 385-436
- In Context : For all you into electronics here’s how you will use complex numbers irl!
- Understanding Questions : Lots of questions to get manipulation in your head
- More Involved : Lots more questions with a bit more thinking.
- Even More Involved : Lots of nice manipulation, you can ignore loci, transformations if you want a bit of fun. Some complex series as well - remember 5b…
- Visual Questions : Further questions, with visual explanations and sketching (which we may know examiners to love…)