Ordinary Differential Equations Tutorial Sheet, Sheet #7

Learning targets



Additional Resources

Tutorials

Software



Problem sheet

Skill Building Questions

Problem 1.

Find the general solutions of the following differential equations. This is very easy to do with WolframAlpha (or similar), but it’s worth understanding how it works.

(a) $\frac{d^2y}{ {dx}^2}-3\frac{dy}{dx}+2y=0$

As the equation is a homogeneous ODE:
$\Rightarrow r^2-3r+2=0,\quad r_{1,2}=1, 2$.
The equation has 2 real roots, so the general solution is:
$\boxed{y(x)=C_1e^x+C_2e^{2x}}$
Using $r_{1,2}$:
$\Rightarrow{} y(x)=C_1e^{1x}+C_2e^{2x} $
Using WolframAlpha:
Click here for WolframAlpha link (you might need to scroll a bit to find the answer)



(b) $\frac{d^2y}{ {dx}^2}+2\frac{dy}{dx}+2y=0$

$\Rightarrow{}\quad$ $r^2+2r+2=0, \quad r_{1,2}=-1\pm i$
$\Rightarrow{}\quad$ One repeated imaginary root, so the general solution is:
$y(x)=C_1e^{-x}\cos{x}+C_2e^{-x}\sin{x}$
$\Rightarrow{}$ Simplified: $\boxed{y(x)=e^{-x}(C_1\cos{x}+C_2\sin{x})}$



(c) $\frac{d^2y}{ {dx}^2}+4\frac{dy}{dx}+4y=0$

$r^2+4r+4=0, \quad r_{1,2}=-2$ (real repeated root)
Therefore, the general solution is:
$y(x)=C_1e^{-2x}+C_2e^{-2x}x $, where the final $x$ appears because the root $-2$ is repeated 2x. Have a look at part (d): the same logic applies there, but for 3 repeated roots.
$\Rightarrow{} $Simplified: $\boxed{y(x)=(C_1+C_2x)e^{-2x}}$



(d) $\frac{d^3y}{ {dx}^3}+6\frac{d^2y}{ {dx}^2}+12\frac{dy}{dx}+8y=0$

This is a scary third-order ODE, but the way we solve it is exactly the same.
$\Rightarrow r^3+6r^2+12r+8=0, \quad \rightarrow \quad r_{1,2,3}=-2$ (for all three)
Therefore, the general solution is:
$ y(x)=C_1e^{-2x}+C_2e^{-2x}x+C_3e^{-2x}x^2 $
where the $x$ and $x^2$ appear because the root $-2$ is repeated 3 times.
$\Rightarrow{}$ Simplified: $\boxed{y(x)=(C_1+C_2x+C_3x^2)e^{-2x}}$



Problem 2.

The differential equation $\ddot{x}+2\dot{x}+4x=0$ describes the free vibration of a mass-spring-damper system, where $x(t)$ represents the displacement from equilibrium of mass $M$.

(a) What values of mass $M$, spring stiffness $k$ and the viscous damping coefficient $c$ does the equation represent?

You can read these straight off the equation. For $\ddot{x}+2\dot{x}+4x=0,$ $\boxed{\text{ Mass } M = 1 \text{, damping coefficient } c = 2 \text{ and spring stiffness } k=4.}$


(b) Show that the frequency of vibration of the system is $\sqrt{3}$ rad/s and verify that this is equal to $\sqrt{\left(4kM-c^2\right)}/2M$.

The auxiliary equation can be written as $mr^2+cr+k=0$.
As $c = 2, k = 4$ & $m = 1$, $r^2+2r+4=0$.
Solving for homogeneous ODE:
$\Rightarrow{}\ r_{1,2}=\frac{-2 \pm \sqrt{2^2 - 4 * 1 * 4}}{2 * 1}$ (the quadratic formula),
$\Rightarrow{} r_{1,2} =-1\pm \sqrt{3} i$
The frequency of an ODE is the imaginary component of the solution of the auxillary equation, i.e. frequency $\boxed{\omega = Im(r) = \sqrt{3}.}$
Note that frequency cannot be negative.
$\Rightarrow{} $ Substituting the values of $c,\ k\ \mathrm{and}\ m$ in (this is trivial in WolframAlpha)
$\boxed{\sqrt{\left(4kM-c^2\right)}/2M = \sqrt{3}, Q.E.D}$








Exam Style Questions

Problem 3.

This graph shows the velocity vs time (purple) and acceleration vs time (red) for a damped harmonic oscillator.

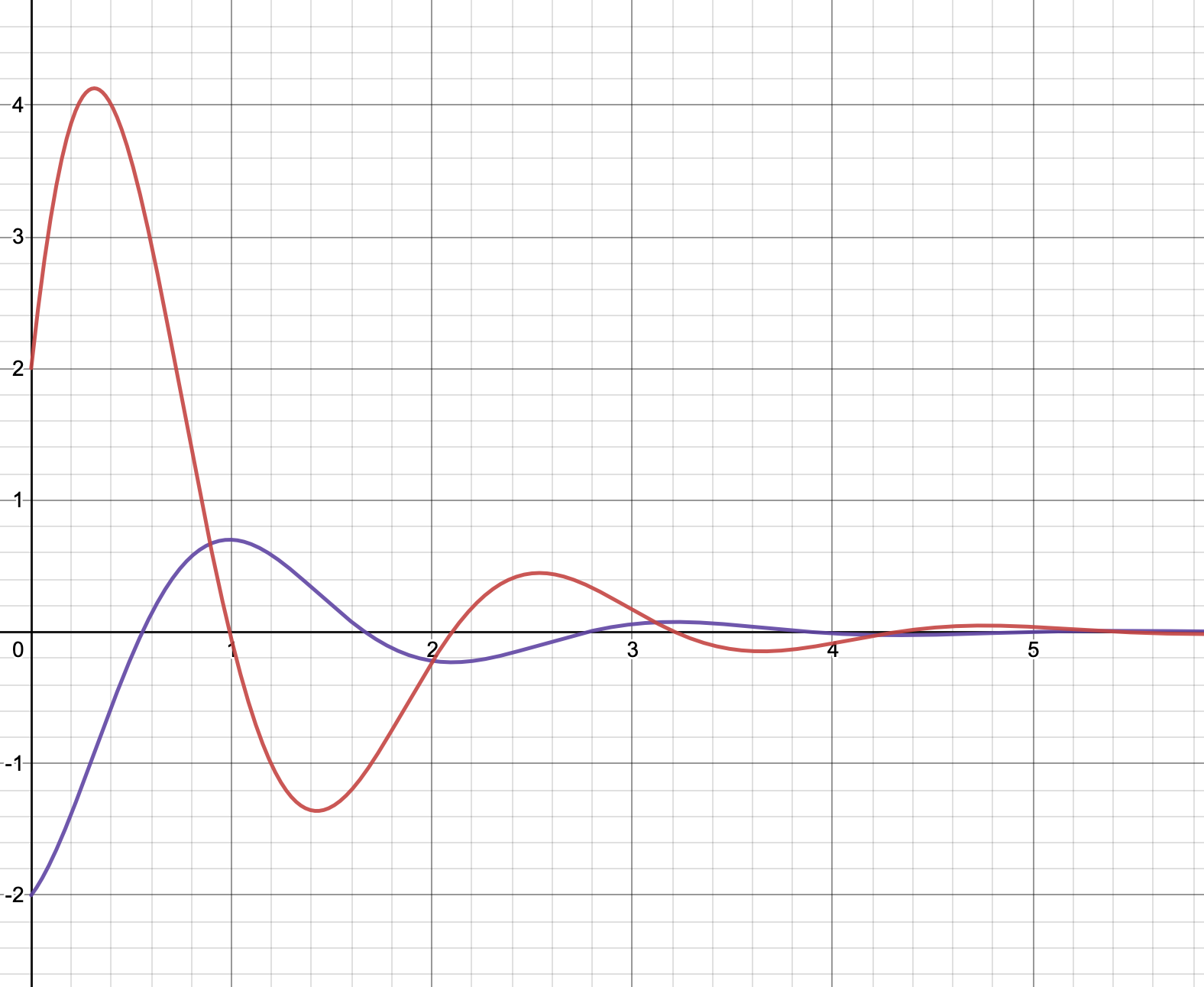
(a) State whether this system is under, over, or critically damped.

The waveform is decaying over time, but does oscillate. Therefore, $\boxed{\text{the system is under-damped.}}$
No working is needed.

(b) Write down the initial velocity and acceleration of the trolley.

Reading off the graph,
$\boxed{v=-2m/s, a=2m/s}$

(c) Find the integer frequency of oscillation of the system, in rad/s.

From the graph, it seems that the time period of oscillation $T ≈ 2.1$s.
Damped natural frequency $\omega = \frac{2\pi}{T} ≈ \frac{2\pi}{2.1}$ $\omega ≈ 2.992$, so we can say that $\boxed{\omega = 3\text{rad/s}}$





Problem 4.

A trolley of mass, $m=$ 5kg, is attached to a wall by a spring of stiffness $k=$ $10Nm^{-1}$ and rolls along the floor with a drag coefficient $c=3$.

At $x=0$ the spring is in its neutral position (neither extended nor compressed) and the positive $x$ direction is considered to be pointing away from the wall. Air resistance can be neglected.

(a) Draw a diagram of this system.


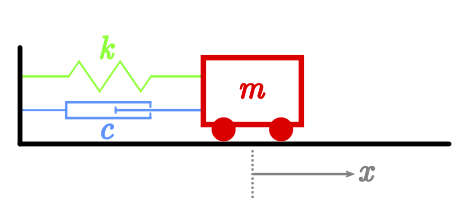
$m=$ 5kg, $k=$ 10Nm$^{-1}$, $c=3$, and $x(0) = 0$








(b) Write an expression relating the location of the trolley to its acceleration.

$m\ddot{x}+c\dot{x}+kx=0$
Using the above values for $m$, $k$ & $c$:
$\quad\Rightarrow\quad \boxed{5\ddot{x}+3\dot{x}+10x=0}$


(c) State whether this system is underdamped, critically damped or overdamped.

$b^2-4ac$ $,\quad 3^2-(4\times 5 \times 10) = 9 - 200 = -191$ $\Rightarrow \boxed{\text{Under-damped}}$



(d) Using this information, sketch a graph of displacement $x$ vs time $t$ for the trolley.

This is something that WolframAlpha is really good at. From your knowledge of what 'under-damped' means, you should have a rough idea of what you're expecting - this will help because you'll know whether Wolfram has given you a sensible answer or not.
Just type the equation and initial conditions into the search: 
5x''+3x'+10x=0, x(0)=0

One of its many outputs will be a ready-made graph:

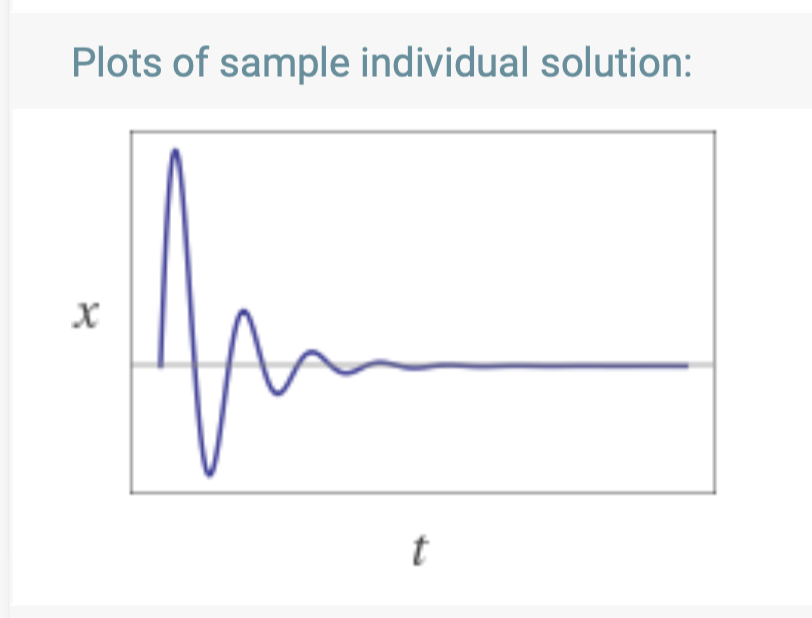
Click here for WolframAlpha link








Problem 5.

A cargo barge of mass $1000$ tonnes ($=1\times10^6\text{kg}$) is anchored to the seabed by a chain that we can assume to behave elastically. The chain has length $L=10m$ and a cross-sectional area $A$ of $0.0002m^2$. The Young’s Modulus $E$ of steel is $210\text{GPa}$, and spring constant $K=\frac{E\times{A}}{L}$.

(a) Find the spring constant $K$.

$K=\frac{E\times{A}}{L}=\frac{210\times10^9\times{0.0002}}{10}$
$\boxed{=4.2\times10^6}$




The anchored barge is hit by a wave, causing it to oscillate on its chain. The water around the barge has a damping effect on the barge, with a damping coefficient $c=2\times10^6$. The below graph shows the barge’s velocity vs time (green) and acceleration vs time (red). The y-intercept of the green line is $-2$ and the red line is $\frac{4}{3}$.

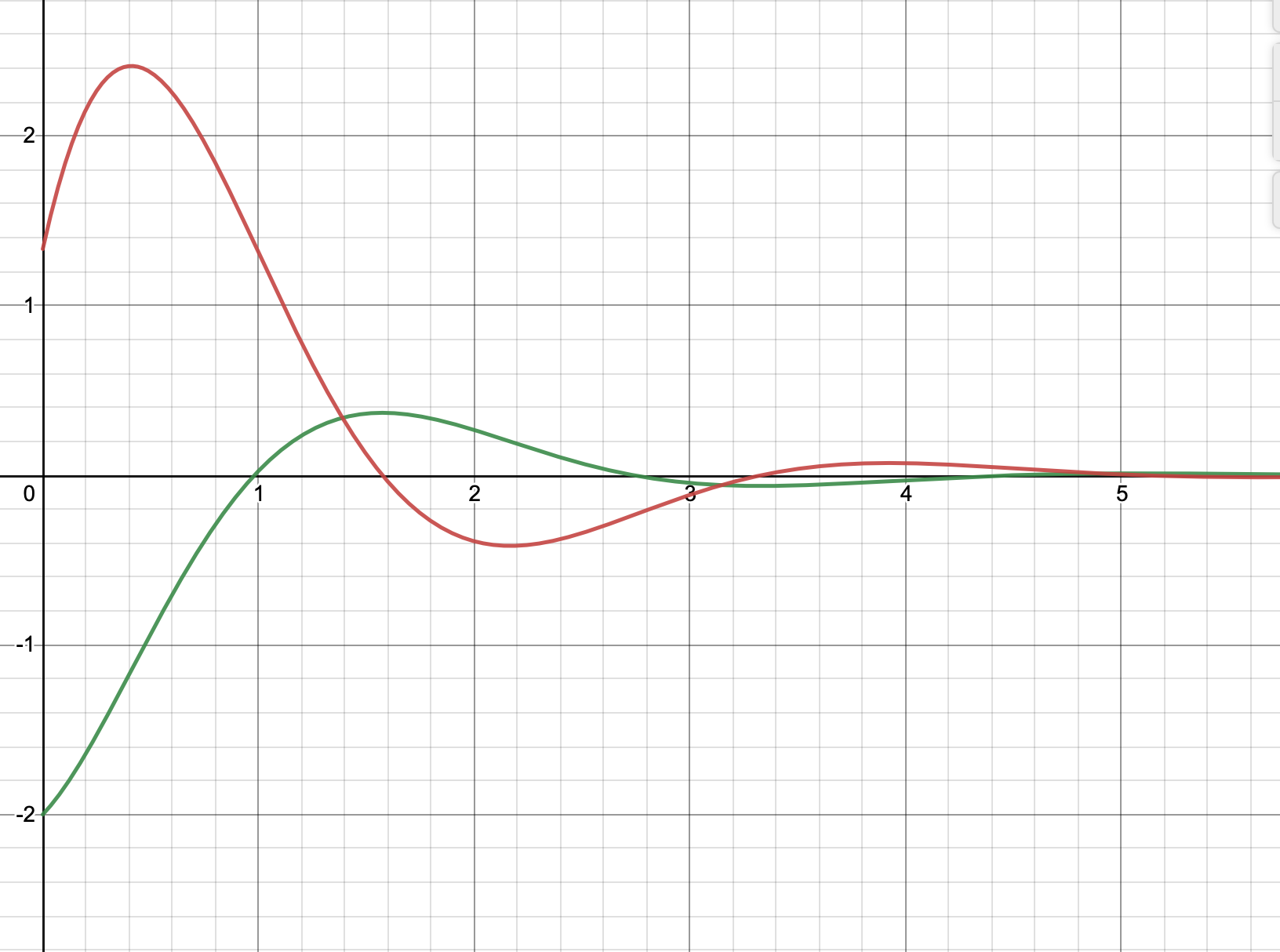
(b) State and explain whether this system is under-, over-, or critically damped.

$\boxed{\text{Underdamped. The system makes several oscillations before coming to rest.}}$


(c) Construct an ODE to describe the motion of the barge.

Using $m$, $c$ & $k$:
$\boxed{1\times10^6\ddot{x}+2\times10^6\dot{x}+4.2\times10^6x=0}$




(d) Find the height of the wave that displaced the barge to start the oscillation.

The question is asking you to find the value of $x$ at $t=0$, (i.e. find $x(0)$).
Using the above equation and the initial conditions from the graph,
$10^6\ddot{x}+2\times10^6\dot{x}+4.2\times10^6x=0,\quad\ddot{x}(0)=\frac{4}{3},\quad\dot{x}(0)=-2$
We can solve this as we would any other ODE. We have 2 initial conditions, so we can build an equation for $x(t)$, and then solve for $t=0$.
We can do this very easily in WolframAlpha
$\Rightarrow$ Tell Wolfram what you know, separating the initial conditions with commas. 
(1x10^6)x''+(2x10^6)x'+(4.2x10^6)x=0, x''(0)=(4/3), x'(0)=-2

$\Rightarrow$ Wolfram will solve the ODE for you.
This isn't a particularly nice way of writing the equation - but that doesnt matter.
We now have a Wolfram solution to this ODE. All we have to do now is plug $t=0$ into the equation:
$\Rightarrow$ Plug the equation back into Wolfram.
You can do this by clicking on it. Then add ", t=0" to the end of the query and press enter. This tells Wolfram that you want the value of the equation at $t=0$.
$\Rightarrow \boxed{x(0)=0.635m}$
$\Rightarrow$ This means that the barge was lifted by a 63.5cm high wave.












WolframAlpha

You can generate a limitless suppply of these second order homogeneous ODE questions and answers using WolframAlpha including the various graphs. For example, try typing in:

3x”(t)+3x’(t)+4x(t)=0 where x(0)=3, x’(0)=0,

Click here for WolframAlpha link



Answers



For Printing



Revision Questions

The questions included are optional, but here if you want some extra practice.

Next week, Coupled Harmonic Oscillators!